Dynamic Programming Matrix Chain Multiplication Example
Lets take the example of the Fibonacci numbers. With this representation we can safely say that Miiis 0 as there is no cost to multiply only one matrix.

Dynamic Programming Matrix Chain Multiplication Optimal Triangulation Csc 252 Algorithms Haniya Aslam Slideshow And Powerpoint Viewer Presentation Overview Understanding Dynamic Programmin
Then ABC 10305 10560 1500 3000 4500 operations ABC 30560 103060 9000 18000 27000 operations.

Dynamic programming matrix chain multiplication example. References 2Matrix Chain Multiplication Problem Matrix chain multiplication or the matrix chain ordering problem is an optimization problem concerning the most efficient way to. Assume that the matrix dimensions allow multiplication in order Matrix multiplication is associative. The chain matrix multiplication problem involves the question of determining the optimal sequence for performing a series of operations.
Dynamic programming method is used to solve the problem of multiplication of a chain of matrices so that the fewest total scalar multiplications are performed. We are given the sequence 4 10 3 12 20 and 7. Start with for loop with L2.
Matrix Chain Multiplication with C Program Example Matrix chain multiplication or Matrix Chain Ordering Problem MCOP is an optimization problem that can be solved using dynamic programming. M1 N-1will be the solution to the matrix chain multiplication problem. Matrix-chainij IF i j THEN return 0 m 1 FOR k i TO j 1 DO q Matrix-chainik Matrix-chaink 1j p i 1 p k p j IF q m THEN m q OD Return m END Matrix-chain Return Matrix-chain1n Running time.
We know M i i 0 for all i. The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7. A_1A_2 A_3 A_1 A_2A_3 A product is unambiguous if no factor is multiplied on both the left and the right and all factors are either a single matrix or an unambiguous product in parentheses.
Example of Matrix Chain Multiplication. Step2 for i in range 1 to N-1. We compute the optimal solution for the product of 2 matrices.
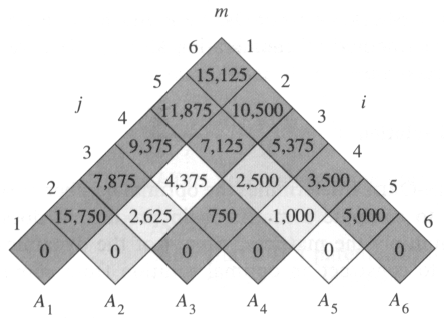
Compute the value of an optimal solution in a bottom-up fashion. The chain matrix multiplication problem is perhaps the most popular example of dynamic programming used in the upper undergraduate course or review basic issues of dynamic programming in advanced algorithms class. ABC 20 x 40 x 2 20 x 2 x 60 2 400.
In our case Mijrepresent the minimum cost to multiply a chain of matrices from matrix ito matrix j. We are given a sequence chain A1 A2 Anof nmatrices to be multiplied and we. It is a Method under Dynamic Programming in which previous output is taken as input for next.
A BC 40 x 2 x 60 20 x 40 x 60 48 000 operations. Given a chain A1 A2 A3 A4An of n matrices we wish to compute the product. Here the matrix index represents the multiplication sequence of a set of matrixes and the corresponding value holds the required minimum multiplications.
A is a 20 40 matrix B is a 40 2 matrix and. Step3 for i in range 2 to N-1. Let us proceed with working away from the diagonal.
We need to compute M ij 0 i j 5. Matrix Multiplication Let A be an n x m matrix B an m x p matrix The product of A and B is n x p matrix AB whose ij-th entry is k1 m a ik b kj In other words we multiply the entries of the i-th row of A with the entries of the j-th column of B and add them up. Matrix-chain-multiply A S i j 1if j i 2 then X matrix-chain-multiply A S i S i j 3 Y matrix-chain-multiply A S S i j 1 j 4 1return matrix-multiply X Y 5 else return Ai MCM1 6 XMCM1 S164 YMCM5 6 XMCM1 S141 YMCM2 4 A1 XMCM2 S242 YMCM3 4 A2.
For example suppose A is a 10 30 matrix B is a 30 5 matrix and C is a 5 60 matrix. If A a ij is a p x q matrix B b ij is a q x r matrix C c ij is a p x r matrix. In the Chain Matrix Multiplication Problem the fundamental choice is which smaller parts of the chain to calculate first before combining them together.
Developing a Dynamic Programming Algorithm Step 3. Here Chain means one matrixs column is equal to the second matrixs row always. Algorithm For Matrix Chain Multiplication Step1 Create a dp matrix and set all values with a big valueINFINITY.
Our first example of dynamic programming is an algorithm that solves the problem of matrix-chain multiplication. Tn nX 1 k1 Tk Tn k O1 2 nX 1 k1 Tk On 2 Tn 1 2 2 Tn 2 2 2 2. The important point is that when we use the equation to calculate we must have already evaluated and For both cases the corresponding length of the matrix-chain are both less than.
2n Exponential is. Given a sequence of matrices the goal is to find. C is a 2 60 matrix then.
13 represent the multiplication of sequence from A2 to A4 ie. Only defined for.

Matrix Chain Multiplication Dynamic Programming Youtube
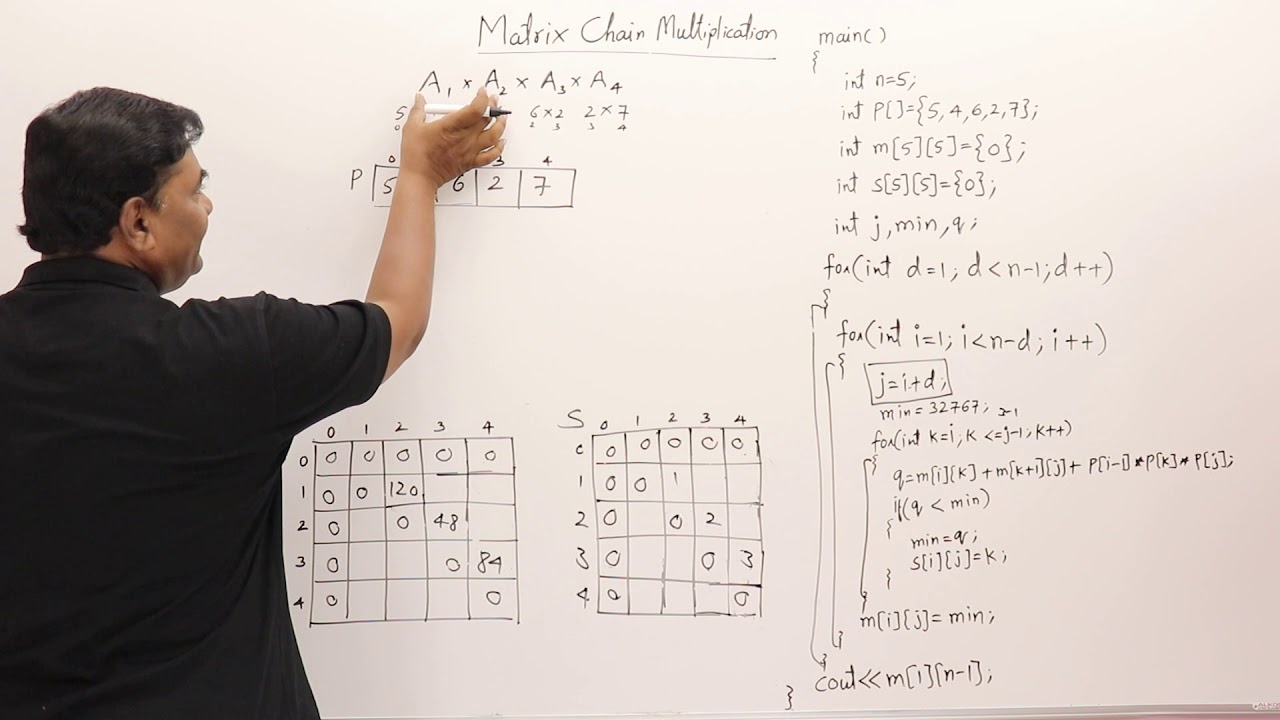
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube
How To Solve Matrix Chain Multiplication Using Dynamic Programming Algorithms Blockchain And Cloud

Matrix Chain Multiplication Matrix Chain Multiplication Is An By Vaibhavi Maradiya Medium

Dynamic Programming Lecture 8 1 Dynamic Programming History

Matrix Chain Multiplication Dp 8 Tutorialspoint Dev

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube

Matrix Chain Multiplication Explained Kilichbek Haydarov

In Java First Create A Chegg Com

Dynamic Programming 3 Example Matrix Chain Multiplication N N What If We Want To Multiply A String Of More Than Two Matrices Together Matrix Course Hero

Matrix Chain Multiplication Problem Using Dynamic Programming Part 1 Youtube

Matrix Chain Multiplication Different Recursive Definition Stack Overflow

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication In C Codespeedy
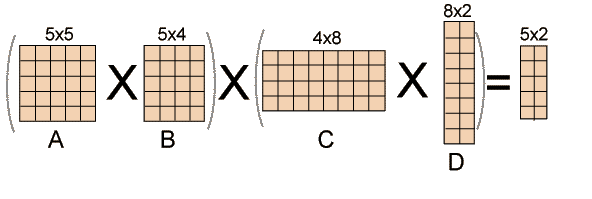
Matrix Chain Multiplication With C Program Example Random Access Memories


