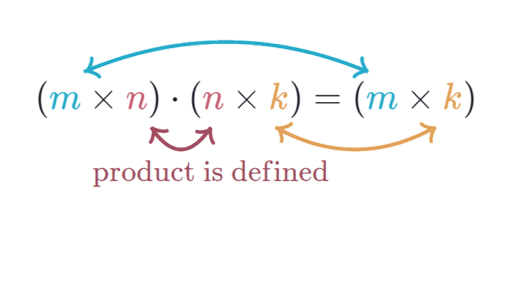Matrix Multiplication Inner Dimensions
As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one. Matrix Multiplication doesnt work for inner dimensions greater than outer in C.
They are not the same number.

Matrix multiplication inner dimensions. Ab times bc will produce ac The product of a matrix and a vector. Now the rules for matrix multiplication say that entry ij of matrix C is the dot product of row i in matrix A and column j in matrix B. To repeat it is good practice and often necessary to think about the dimension of an answer before performing any matrix multiplication.
The general scheme is. The element at row i column j of C is the dot product of row i of A and column j of B. The answer is no solution.
The number of elements in other dimensions of multidimensional matrix product. Make sure that the the number of columns in the 1 st one equals the number of rows in the 2 nd one. The product will be a 24 matrix the outer dimensions.
We can use this information to find every entry of matrix C. Im going off the Create 2-D Line Graph tutorial on Mathworks. 1 C N.
21 Matrix Multiplication Remark When the sizes of A and B are written side by side in the same order as the product that is m nn p the inner dimensions must be equal and the outer dimensions give the size of the product AB. The multiplication is defined because the inner dimensions 3 are the same. First dimension of multidimensional matrix.
If we write this as 3 x 22 x 2 we check the inner dimensions to make sure they match. The number of elements in the second dimension of multidimensional matrix product. The operator is algebraic matrix multiplication also called inner product.
The pre-requisite to be able to multiply Step 2. Consider the matrix multiplication AxB C. For example you can together a 4 x 3 matrix and a 3 x 1 matrix and get a 4 x 1 result.
I am writing a code to multiply matrices of any dimensions. I noticed it works fine for square matrices as well as when the outer dimensions are greater than inner. Multiply the elements of each row of the first matrix by the elements of each column in the second matrix.
When doing so one can also check to make certain that the inner dimensions are the same as is required. It is important that you memorize this rule. For two matrices AB the rule is that size A2 must be the same as size B1 and that the output is size A1 by size B2.
In order to multiply matrices Step 1. Interestingly this means that we cant multiply them in the other order becuase then we have 2 x 23 x 2 and the inner dimensions. For example you can together a 4 x 3 matrix and a 3 x 1 matrix and get a 4 x 1 result.
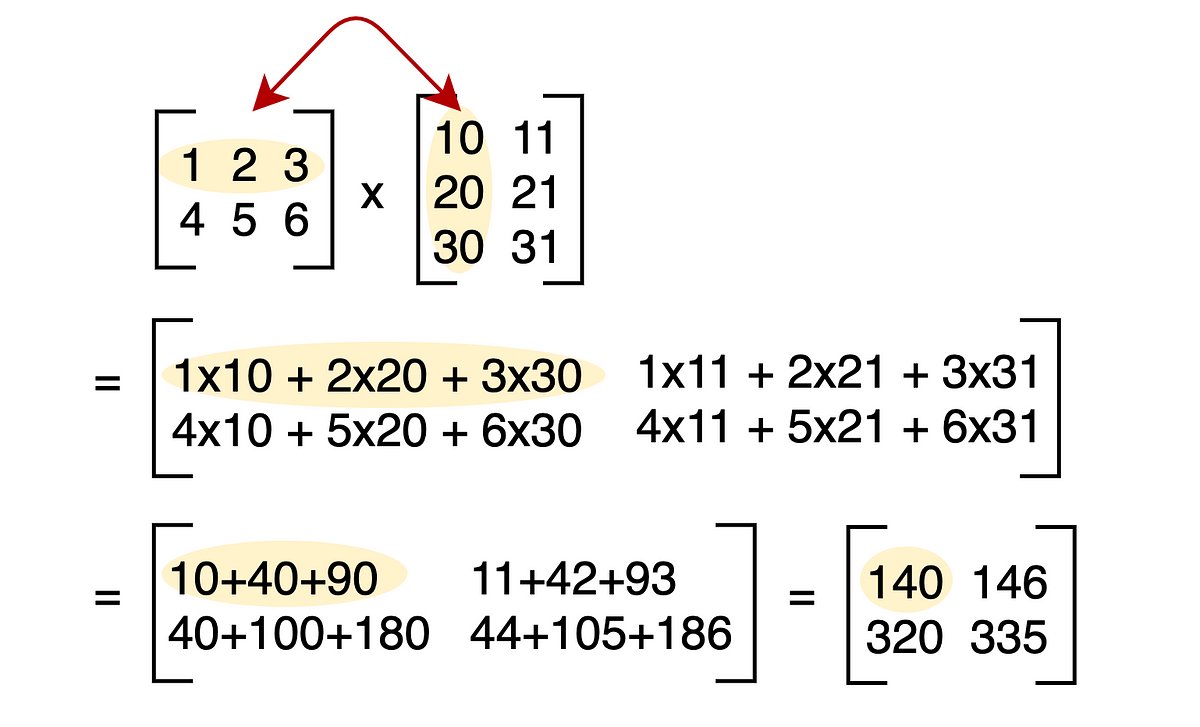
Since there are three columns in the first matrix and three rows in the second matrix the inner dimensions which must be the same each element in the product will be the sum of three products. 3x3 are the same and so viola that should work right and give us our 2x3 resultant matrix. 24 28 22 48 4 32 36.
Y exp -x sin x. The dimensions of our first matrix are 3 x 2 and the dimensions of the second are 2 x 2. For two matrices AB the rule is that sizeA2 must be the same as sizeB1 and that the output is sizeA1 by sizeB2.
X linspace 04pi100. I want to plot f x e -xsin x over the range 0 to 4pi but I get an inner matrix dimensions must agree error on the second line. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one.
In order to multiply two matrices together their inner dimension MUST be the same. However I cant get it to work for cases where outer dimensions are smaller then inner such as multiplying a 2X3 matrix with a 3X2 matrix. It would be easy to simply matrix multiply the two together since the two inner dimensions of Theta.
In matrix multiplication since each of the input matrices can be accessed in either a row-major order or column-major order there are four possible ways to perform matrix multiplication inner product row times column outer product column times row row-wise product row times row and column-. The operator is algebraic matrix multiplication also called inner product. Is equal to the number of elements in the second dimension of multidimensional matrix.
2 C N. In this example the inner dimensions are 4 and 5. Therefore there is no work to be done.
Here are the steps for each entry. For example if you multiply a matrix of n x k by k x m size youll get a new one of n x m dimension. This dot product exists only if the second dimension of the first matrix matches the first dimension of the second matrix.

Matrix Multiplication And Associated Properties Youtube
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
Matrix Multiplication Dimensions Article Khan Academy
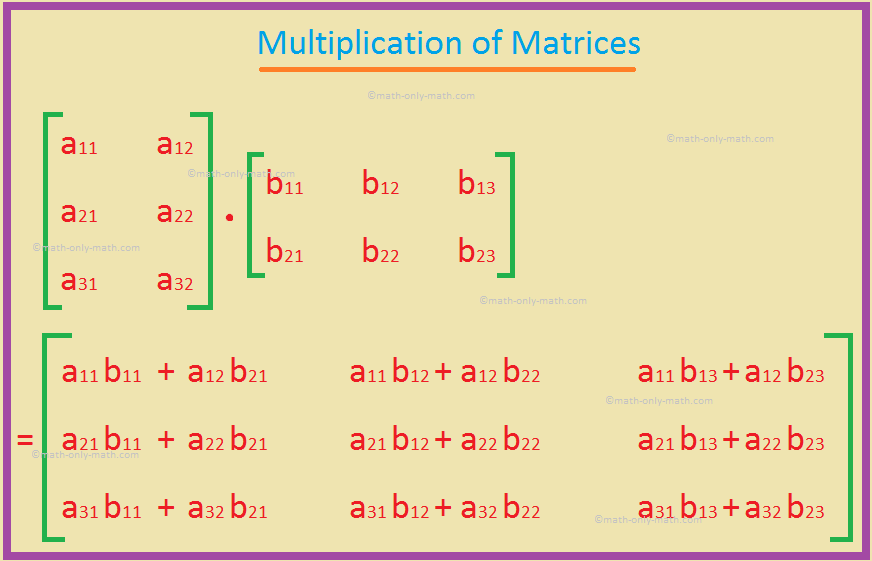
Multiplication Of Matrices How To Multiply Matrices Rules Examples
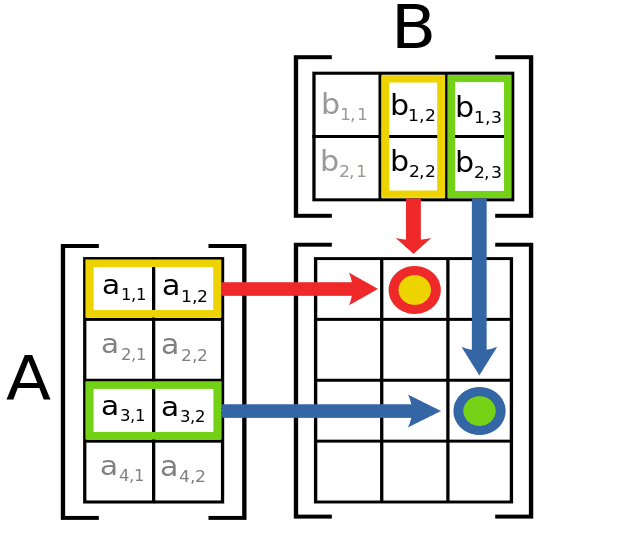
Introduction To Matrices And Matrix Arithmetic For Machine Learning

Equation Of A Circle Notes Interactive Notebook Color Coded Interactive Notebooks Math Lessons Secondary Math

Matrix Multiplication In C Applying Transformations To Images

How To Identify The Best Customers Using Rfm Based Segmentation In 2020 Segmentation Company Goals E Commerce Business
Matrix Multiplication Dimensions Article Khan Academy

Matrices Multiplying Matrices Of Different Sizes Youtube

Matrix Mathematics Linear Transformations Mathematics Linear Map
Matrix Multiplication Dimensions Article Khan Academy

Multiplying Matrices Video Khan Academy