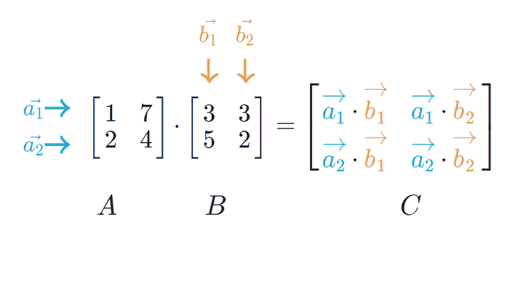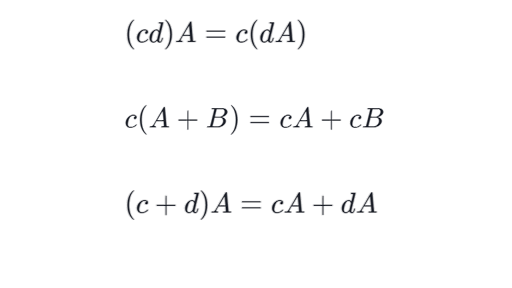Inner Product Of 2x2 Matrix
DetfAg a 11Using this definition as a starting point the determinant of a square matrix A2C nis defined recursively. For x h x1 x2 i y h y1 y2 i 2 R2 deflne hxyi 2x1y1 x1y2 x2y1 5x2y2.

Scalar Multiplication Of Matrices And Matrix Operations Youtube
For matrices the typical definition of the dot product is the Frobenius inner product.

Inner product of 2x2 matrix. We define inner product on V R2x2 by trBA Transpose U is a subspace of V U A V trA 0 How do I find an orthonormal basis for U relative to the given inner product. Secondaly it is also explained how to find out cross product of 3x1 mat. If I understand you right and youre multiplying every element of A by the corresponding element of B then its an inner product.
If latexAlatex is an latextext mtext times text rtext latex matrix and latexBlatex is an latextext rtext times text ntext latex matrix then the product matrix latexABlatex is an. As for the positive deflnite property note that hxxi 2x2 12x x2 5x 2 2 x1 x22 x1 2x22 0. A B C A C B C.
For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix. The cross product of two vectors and is given by. It looks like this.
I am asked to prove that this is indeed an inner product. Orthogonal vectors have inner product zero. Can you show an example with a 2x2 matrix Mansoor Mar 26 at 858 With dot product I mean the sum of the Hadamard produrct or the Frobenius inner product.
Simply compute as if the matrix was a vector. In mathematics particularly in linear algebra matrix multiplication is a binary operation that produces a matrix from two matrices. It is easy to see the linearity and the symmetric property.
A B B A. Below is an example of a 2x2 matrix and 3x2 matrix x a1b1c1d1 y a2b2c2d2e2f2 npinnerxy output a1xa2b1xb2 a1xc2b1xd2 a1xe2b1f2c1xa2d1xb2 c1xc2d1xd2 c1xe2d1xf2. A B C c i k j a i j b j k A B C c i k j a i j b j k Customer Voice.
A B T r a c e A Bwhere AB are 2x2 traceless Hermitian matrices. It goes with the Frobenius norm of the matrix. A dot product inner product is a scalar.
The 2x2 matrix of complex multiplication is an orthogonal matrix because the vectors in it are orthogonal. A A 0 in particular A A 0 A 0. The resulting matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix.
An identity matrix with a dimension of 22 is a matrix with zeros everywhere but with 1s in the diagonal. We go by 3 definitions for inner product. FesslerlicenseAugust 23 2017 262 261 Matrix algebra smatdet 2611 Determinant smatdet If A a 11 2C is a scalar then the determinant of Ais simply its value.
The inner product in this space is defined as. Although this may seem like a strange definition its useful properties will soon become evident. For real matrices beginequation Acdot B equiv sum_i sum_j A_ij B_ij endequation For your pair of 2x2 matrices.
Just to provide you with the general idea two matrices are inverses of each other if their product is the identity matrix. The product AB can be found only if the number of columns in matrix A is equal to the number of rows in matrix B. In this video it is explained how to calculate the dot product of 3x1 and 2x2 matrix.
In order to prove that the above vector space is a Hilbert space we can consider a Cauchy sequence and show that it converges into the space. Then hi is an inner product on R2. Recall that the determinant of a 2x2 matrix is.
I am given a matrix inner product on square matrices defined as A B t r A B t where M t denotes the transpose. Finding the product of two matrices is only possible when the inner dimensions are the same meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. But can we prove it in a.
The vector space V with an inner product is called a real inner product space. While perpendicularity or orthogonality can be visualised for the case of vectors with two components this is impossible for vectors of more than two components. Clearly though it is not clear how I should calculate the outer product of r with itself because now the definition of inner product with transponse and outer product with itself have the same syntax in matlab.
There is an easy way to remember the formula for the cross product by using the properties of determinants. There is a lot difference between inner product and dot product in higher dimensional space. Inner has components 2x24 and this is what I expect from the matrix multiplication of r with its transponse.
Frobenius Norm -- from Wolfram MathWo. Thats the matrix product not the dot product.

Foil Method Math Poster Zazzle Com Math Methods Math Poster Studying Math
Multiplying Matrices Article Matrices Khan Academy

Let V R 2x2 Be The Vector Space Of All 2 X 2 Chegg Com

3 In M2x2 C With Inner Product A B Tr B A A Chegg Com

Intro To Matrices Dont Be Scared What Is
Properties Of Matrix Scalar Multiplication Article Khan Academy
Solved Question 1 7 8 5 A Consider The Inner Product Chegg Com
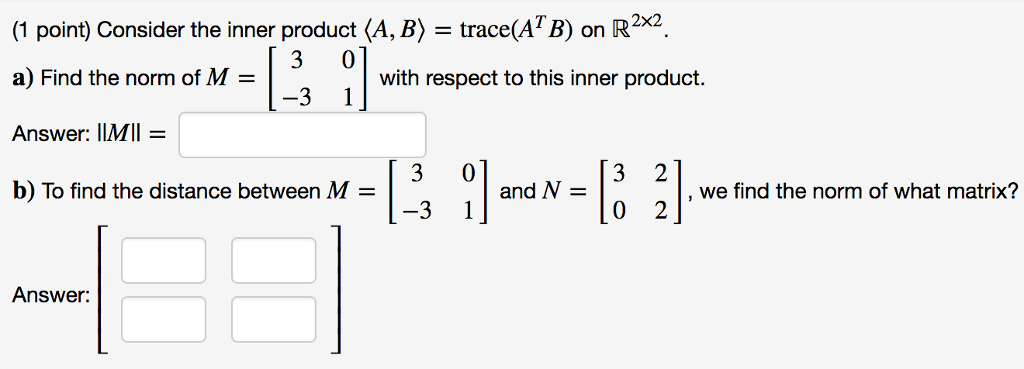
Solved Consider The Inner Product A B Trace A T B O Chegg Com

Lecture 9 Vector Inner Product Space Ppt Video Online Download

1 Point Let M And M 1 Consider The Inner Chegg Com

Consider The Inner Product In The Vector Space Of Matrices R 2x2 Youtube

1st 2 Parts Frobenius Inner Product Youtube

Linear Algebra And Matrices Mallikarjun Department Of Mathematics

Numpy Explains Linear Algebra Programmer Sought

24 Intersections And Sums Of Subspaces Youtube

Thanksci Vi Gauge Symmetries Classical Physics Wave Function Mechanical Wave

Problem 5 Consider The Vector Space M22 Formed By 2x2 Chegg Com