Matrix Nonsingular Proof
Here κ G A refers to any matrix norm. Now we see that IT A1AT ATA1T sinceA1AIsince ABT BTAT.

Why Is A Matrix Invertible If It Can Be Written As The Product Of Elementary Matrices Mathematics Stack Exchange
Prove that if A is an n x n diagonal matrix with nonzero main diagonal elements.

Matrix nonsingular proof. Ifλis to be an eigenvalue then Theorem 21 must hold. A Show that if A is invertible then A is nonsingular. κA T A κA 2.
Then the N x N matrix PTVP is real symmetric and positive semidefinite. However what the theorem says is that we cannot have an non-singular matrix that is nilpotent. B Let A B C be n n matrices such that AB C.
Hence we cannot have an invertible matrix which is nilpotent. Show that if A2 0 then I - A is non-singular and I-A-1 IA. κ G αA κ G A where α 0 is a constant.
If A and B are both n n matrices then detAdetB detAB. A is row-equivalent to I. The matrix I_n is nonsingular since it row-reduces easily to I_ntext Theorem NMRRI.
A matrix A is nonsingular if and only if A is invertible. Let A be a nonsingular matrix. Let A be a nonsingular n n matrix.
Hence A is nonsingular. A square matrix is invertible if and only if its determinant is non-zero. If Every Trace of a Power of a Matrix is Zero then the Matrix is Nilpotent Let A be an n n matrix such that tr A n 0 for all n N.
This video explains what Singular Matrix and Non-Singular Matrix are. The equation adjointUUI_n gets us halfway to an inverse of Utext and Theorem OSIS tells us that then UadjointUI_n also. Since I X T X is positive definite v must be zero.
Therefore we have seen that a matrix is invertible if and only if it is non-singular. The second part is easy for me but how can I show that if A2 0 then I - A is non-singular. That is asubscriptii0 for all 1 i n then A is nonsingular and find Asuperscript-1 A inverse Homework Equations ABBAIsubscriptn The Attempt at a Solution.
A sequence of elementary row operations will reduce A to I. Namely there exist a positive integer m such that A m is the zero matrix. Now suppose A v 0.
A matrix is block diagonally dominant by rows if for a given norm and block partitioning the diagonal blocks are all nonsingular and is block diagonally dominant by columns if is block diagonally dominant by rows. Theorems 114 and 115 tell us how elementary row matrices and nonsingular matrices are related. Then κ A 1 if and only if A T A αI where α 0.
Let A be an orthogonal matrix. κ p A 1 for any p-norm. By definition there exists A1 such thatA1AAA1 IFirst we note thatIT I verify this.
Or is there another easier way. A is a product of elementary row matrices. Prove that if either A or B is singular then so is C.
Write A I X where X S H F G. SDD then it is nonsingular by Theorem 11 and as a resultλis not an eigenvalue. I found in Wolfram Alpha that A matrix is singular iff its determinant is 0 but how I can relate this to the given A2 0.
The proof of Theorem 2. Then I X v 0 X v v v T X T X v v T v and hence v T I X T X v 0. To learn more about Matrices enroll in our full course now.
C Show that if A is nonsingular then A is invertible. Recall that a matrix is singular if its determinant is 0 and non-singular otherwise. The given condition means that I X T X is positive definite.
κ 1 A κ A T. If and only if P is nonsingular Proof. If the blocks are all then block diagonal dominance reduces to the usual notion of diagonal dominance.
Otherwise the system Ax 0 would have a non-trivial solution. To determine if a matrix has this property nonsingularity it is enough to just solve one linear system the homogeneous system with the matrix as coefficient matrix and the zero vector as the vector of constants or any other vector of constants see Exercise MMT10. Then prove that A is a nilpotent matrix.
So by Theorem NPNF U and adjointU are both nonsingular matrices. Add to solve later. κA κA T.
Theorem C5 Let the real symmetric M x M matrix V be positive semidefinite and let P be a real M x N matrix. Use the multiplicative property of determinants Theorem 1 to give a one line proof that if A is invertible then detA 6 0. The proof follows from Theorem 24 by taking the positive definite M x M matrix V as the identity matrix of order M.

Solved 6 Prove That Any Two Nonsingular N X N Matrices A Chegg Com

Exercise 7 24 Marks Prove Or Disprove 1 Let A Be Chegg Com

17 Let A Be Any Nx N Nonsingular Matrix B Be Any Chegg Com

How To Prove A Matrix Is Nonsingular In 10 Seconds Problems In Mathematics

Prove Rank Ap Rank A If P Is An Invertible N N Matrix And A Is Any M N Matrix Mathematics Stack Exchange
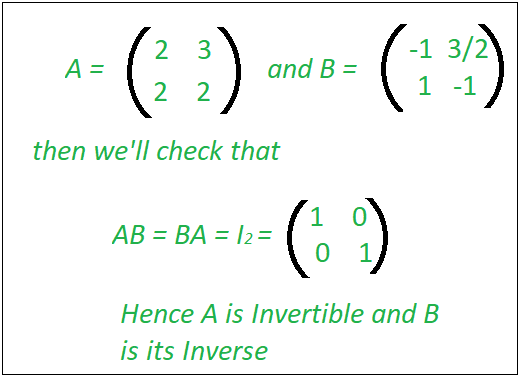
Check If A Matrix Is Invertible Geeksforgeeks

Properties Of The Inverse Matrix

Prove That If A Is Nonsingular Matrix And Ab 0 Then B Is Null Matrix Proof Youtube

To Prove A Matrix Non Singular Mathematics Stack Exchange

Why Can All Invertible Matrices Be Row Reduced To The Identity Matrix Mathematics Stack Exchange

Linear Algebra Ch 2 Determinants 23 Of 48 Non Invertible Matrix Example Youtube

Linear Algebra Lecture 25 The Invertible Matrix Theorem Youtube

Invertible Matrix Theorem Youtube

Singular Matrix Video Lessons Examples And Solutions

Ex Determine If A 3x3 Matrix Is Invertible Nonsingular Using A Determinant Youtube

Inverse Of A Non Singular Square Matrix Solved Example Problems

Confused About Elementary Matrices And Identity Matrices And Invertible Matrices Relationship Mathematics Stack Exchange

Determinant Theorems And Proofs Part 3 Of 4 Invertible Youtube

7 Section 2 7 24 Prove That If A Square Matrix A Chegg Com