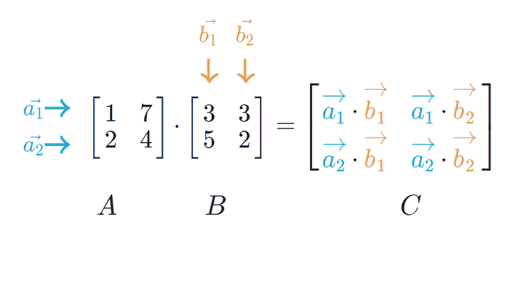Multiplication Of Matrices Linear Combination
Then the matrix product of A A with B B is the mp m p matrix where column i i is the matrix-vector product ABi A B i. Transformations and matrix multiplication.
Multiplying Matrices Article Matrices Khan Academy
Notice the dimensions or shapes.
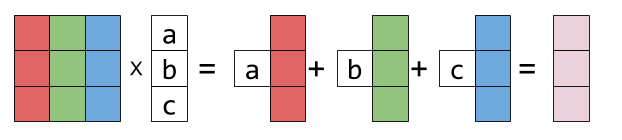
Multiplication of matrices linear combination. 4 3 6 0 3 2 5 4 5 7 4 9 Share. 3 4 2 3 7 5 6 4 5 3 4 5 0 4 4 3 9 5 So the third column represented as a linear combination of columns of A is given by. So this definition takes an equal number of scalars and vectors combines them using our two new operations scalar multiplication and vector addition and creates a single brand-new.
Row Vector Times a Matrix Linear combination of rows Suppose a a1 an is a 1-by-n matrix and C is an n-by-p matrix. Suppose A A is an mn m n matrix and B1B2B3Bp B 1 B 2 B 3 B p are the columns of an np n p matrix B B. In other words aC is a linear combination of the rows of C with the scalars that multiply the rows coming from a.
Visualizing matrix multiplication as a linear combination. Now we can define the linear transformation. This is the currently selected item.
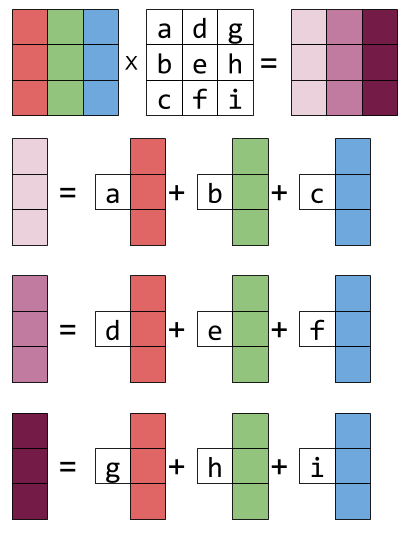
Simply5a linear combination of the columns v1A1v2A2 vnAn. This means you take the first number in the first row of the second matrix and scale multiply it with the first coloumn in the first matrix. Given n n vectors u1u2u3un u 1 u 2 u 3 u n from Cm C m and n n scalars α1 α2α3αn α 1 α 2 α 3 α n their linear combination is the vector α1u1α2u2 α3u3αnun α 1 u 1 α 2 u 2 α 3 u 3 α n u n.
Corollary 6Matrix multiplication is associative. That is ifC BandAarematrices with the correct dimensions thenCBACBA. Then aC a1C1 anCn.
Edited Oct 21 13 at 1952. If A is an mxn matrix latexA vecv_1 vecv_2 dots vecv_nlatex then latexvecxlatex must be an n-dimensional vector and the product latexAvecxlatex will be an m-dimensional vector. 3 1 8 4 5 1 9 7 3 8 4 5 1.
And left-multiplying by a matrix is the same thing repeated for every result row. Hlo everyoneIn this video I have discussed on the Chapter Algebra of matrices Topics-Representation of matrixmatrix addition and scalar multiplication. Compositions of linear transformations 1.
Answered Oct 21 13 at 1941. Multiplying A by B is the linear combination. Then is a matrix equation that corresponds to our system of equations.
Distributive property of matrix products. Created by Sal Khan. We multiply rows by coloumns.
Solving this equation is equivalent to ndingx1andx1such that thelinear combination of columns of Agives the vectorb. You do this with each number in the row and coloumn then move to the next row and coloumn and do the same. Introduction to compositions of Linear Transformations.
A matrix is a linear combination of if and only if there exist scalars called coefficients of the linear combination such that In other words if you take a set of matrices you multiply each of them by a scalar and you add together all the products thus obtained then you obtain a linear combination. Definition MM Matrix Multiplication. While its the easiest way to compute the result manually it may obscure a very interesting property of the operation.
Theorem 7IfAandBarennmatrices such thatBAInthe identitymatrix thenBandAare invertible andBA1. The product of a matrix A by a vector y will be the linear combination of the columns of A using the components of y as weights. Each result cell is computed separately as the dot-product of a row in the first matrix with a column in the second matrix.
It becomes the linear combination of the rows of x with the coefficients taken from the rows of the matrix on the. Observe that each component of the product vector corresponds to one of the equations in the system. So the third column of matrix A B is given by.
Consider the linear system Lets construct the coefficient matrix and multiply it by on the right. When multiplying two matrices theres a manual procedure we all know how to go through. The implication for the matrix productABis that each of its columnsABj is alinear combination of the columns ofA with coe.
Compositions of linear transformations 2. OfA with the scalars multiplying these columns taken in order from top to bottomfromv. The number of columns of Amust beequal to the number of rows of xto do the multiplication and the vectorwe get has the dimension with the same number of rows as Aand the samenumber of columns asx.
In general a system of linear.

An Intuitive Guide To Linear Algebra Betterexplained Algebra Matrix Multiplication Linear

Linear Algebra Tutorial Algebra Learning Math Polynomials
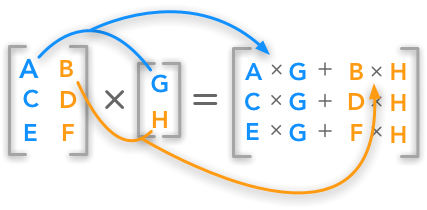
Introduction To Matrices And Vectors Multiplication Using Python Numpy
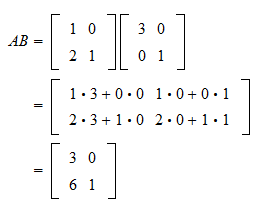
Matrix Multiplication And Linear Combinations

Matlab Video Tutorial Multiplying Matrices And Vectors Youtube

What Does Span Mean In Linear Algebra Algebra Linear Math

Nonsquare Matrices As Transformations Between Dimensions Essence Of Li Algebra Matrix Multiplication Matrix

Visualizing Matrix Multiplication As A Linear Combination Eli Bendersky S Website Matrix Multiplication Multiplication Linear

Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
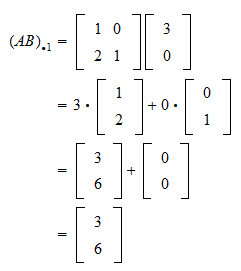
Matrix Multiplication And Linear Combinations
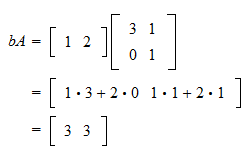
Matrix Multiplication And Linear Combinations
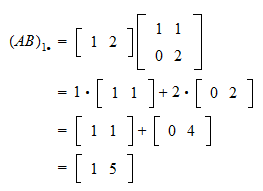
Matrix Multiplication And Linear Combinations

Matrix Element Row Column Order Of Matrix Determinant Types Of Matrices Ad Joint Transpose Of Matrix Cbse Math 12th Product Of Matrix Math Multiplication
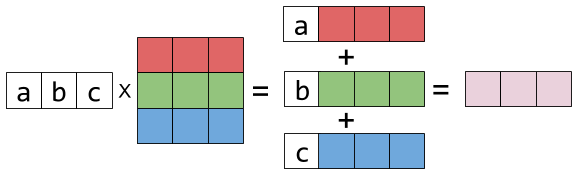
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data