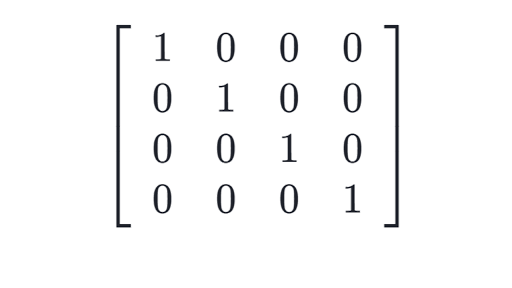Matrix Multiplication Low Rank
You can also truncate the SVD of a higher-rank matrix to get a low-rank approximation. The calculator will find the product of two matrices if possible with steps shown.

Pin On Practices Rule Of Life Via Liveshapes
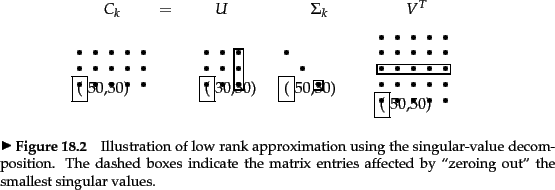
More specifically if an m n matrix is of rank r its compact SVD representation is the product of an m r matrix an r r diagonal matrix and an r n matrix.

Matrix multiplication low rank. Approximating matrix multiplication and low-rank approximation Lecturer. Up to 10 cash back Tile low-rank general matrix multiplication TLR GEMM is a novel method of matrix multiplication on large data-sparse matrices which can significantly reduce storage footprint and arithmetic complexity under given accuracy. We approximate the productA B using two sketches Ae Rtm.
Remember that the rank of a matrix is the dimension of the linear space spanned by its columns. 5 where x 2Cmrepresents a vectorized array of the k-space data to be recovered Tx is a structured lifting of x to a matrix in CM N and b are the known k-space samples. The memory cost and matrix-vector multiplication complexity are quasi-linear with respect to the de-grees of freedom DOFs in the problem.
M 1M 2M tM γ P 1 t t i1 M i. KAAT BBTk kAATk 2Small B2Rd and d 3Computationally easy to obtain from A. Copper-smith and Winograd showed that the asymptotic rank of CW q is as low as possible given its dimensions.
Proposition Let be a matrix and a square matrix. Copies of a self-adjoint random matrix M of size n with as. Shortly after introducing H-matrix Hackbusch et al.
Min x rankTx st. It multiplies matrices of any size up to 10x10 2x2 3x3 4x4 etc. A large direct sum of matrix multiplication tensors.
In this work we focus on the case where Tx is a Toeplitz-like matrix encoding a convolution relationship of the form Txh P. Low Rank Matrix-valued Chernoff Bounds and Approximate Matrix Multiplication Avner Magen Anastasios Zouzias Abstract In this paper we develop algorithms for approximating matrix multiplication with respect to the spectral norm. The matrix-vector multiplication with submatrices and the low-rank update of submatrices.
If r is constant you can multiply this by a. Rank one VR07 Low Rank MZE M 2. Low rank in the context of LRA refers to the inherent dimension of the matrix which may possibly be much smaller than both the actual number of rows and columns in the matrix.
Conditions a low-rank matrix can be sensed and recovered from incomplete inaccurate and noisy observations. Presses operators restricted to far-range interactions by low-rank matrices. The border rank of the matrix multiplication operator fornnmatrices is a stan-dard measure of its complexity.
We consider three such schemes one based on a condition called the Restricted Isometry Property RIP for maps acting on matrices which is reviewed in section II and two based on directly sensing the row and column space of the matrix. Matrix Approximation Let PA k U kU T k be the best rank kprojection of the columns of A kA PA kAk 2 kA Ak 2 1 Let PB k be the best rank kprojection for B kA PB kAk 2 1 q 2kAAT BBTk FKV04 From this point on our goal is to nd Bwhich is. Using techniques from algebraic geometry and representationtheory we show the border rank is at least 2n2 n.
Let A Rnm and B Rnp be two matrices andε0. If is full-rank then. ρ2 M x x E M 1 1polyn 1polyn 1polyt exp.
Thus a matrix may be approximated if not exactly represented by another matrix containing signi cantly less rows and columns while still preserving the salient. Since the work of Coppersmith and Winograd CW90 the fastest matrix multiplication algorithms have used T CW q the Coppersmith-Winograd tensor. We derive a fast algorithm for the structured low-rank matrix recovery problem.
Another important fact is that the rank of a matrix does not change when we multiply it by a full-rank matrix. C ε2t γ log t Oγ logγε2ε2 Oγ logγε2ε2 rank MO1 E M1 Let be iid. Our bounds are better than the previouslower bound.
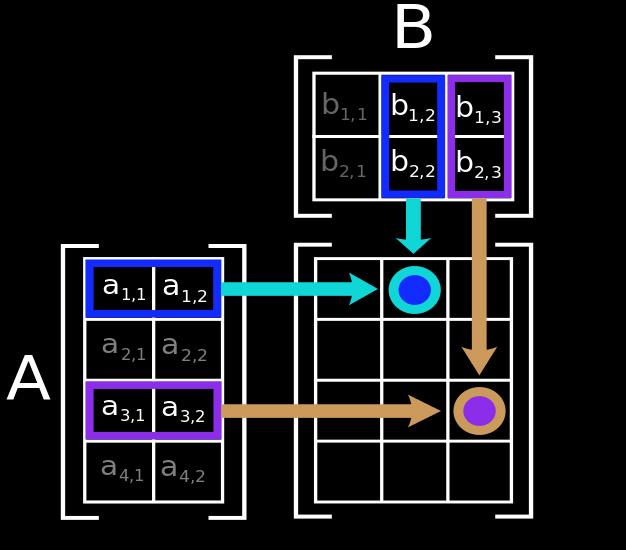
The proposed multi-scale low rank decomposition is well motivated in practice since natural data often exhibit multi-scale structure instead of globally or sparsely. 23 again introduced H2-matrix which uses nested low-rank bases to further re-. Richa Bhayani and Daniel Chen Unedited notes 1 Matrix Multiplication using sampling Given two matrices Aof size m nand Bof size n pour goal is to produce an approximation to the matrix multiplication product AB.
P x b. While the matrix-vector multiplication is straightforward implementing efficient low-rank updates with adaptively optimized cluster bases. Concretely we propose a multi-scale low rank modeling to represent a data matrix as a sum of block-wise low rank matrices with increasing scales of block sizes.
Multiplication by a full-rank square matrix preserves rank. Arithmetic operations like multiplication inversion and Cholesky or LR factorization of H 2-matrices can be implemented based on two fundamental operations.

Algorithms For Big Data Compsci 229r Youtube Algorithm Big Data Lecture
Identity Matrix Intro To Identity Matrices Article Khan Academy

Determine Order Of Matrix Matrix Multiplication Examples
Explained Matrices Mit News Massachusetts Institute Of Technology
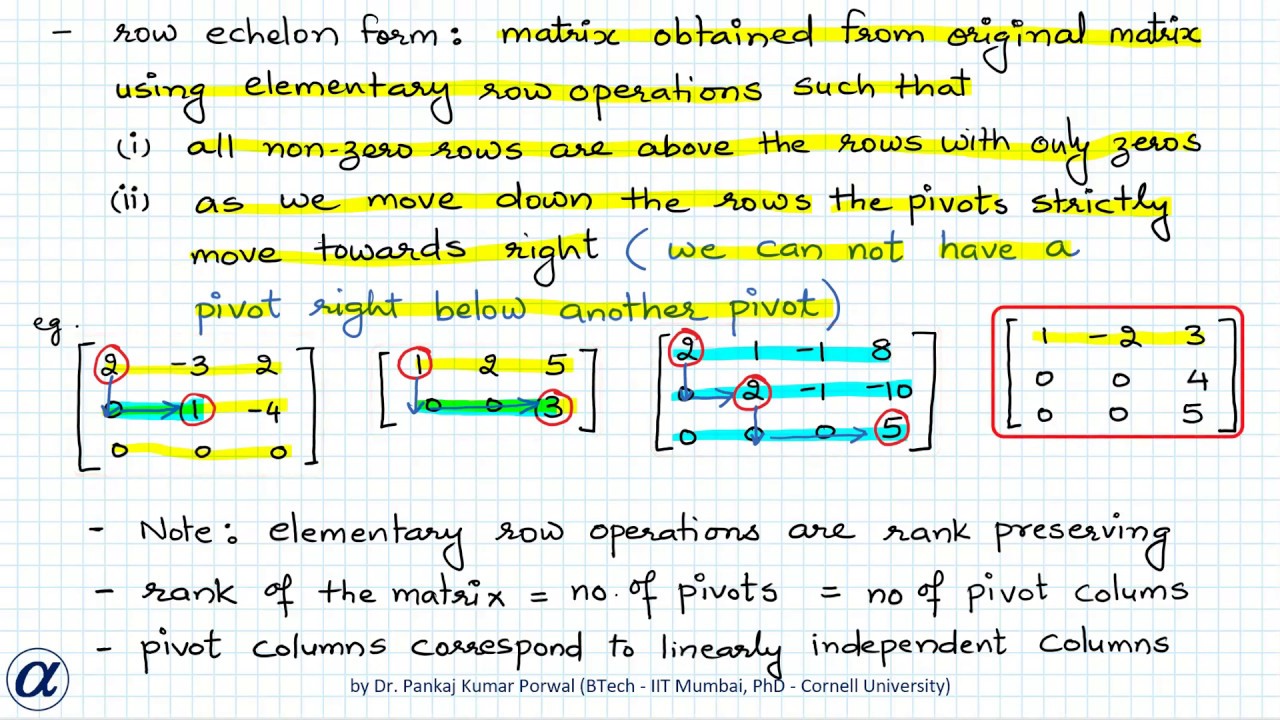
Rank Of A Matrix And Methods To Find The Rank Minor Method And Row Echelon Form Method Youtube

Matrix Multiplication An Overview Sciencedirect Topics

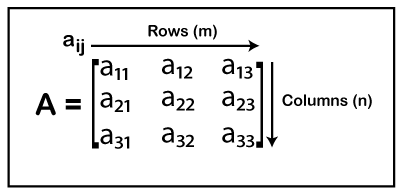
Introduction To Matrices Boundless Algebra

What Is The Meaning Of Low Rank Matrix Quora

Nonsquare Matrices As Transformations Between Dimensions Chapter 8 Essence Of Linear Algebra Youtube

Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange
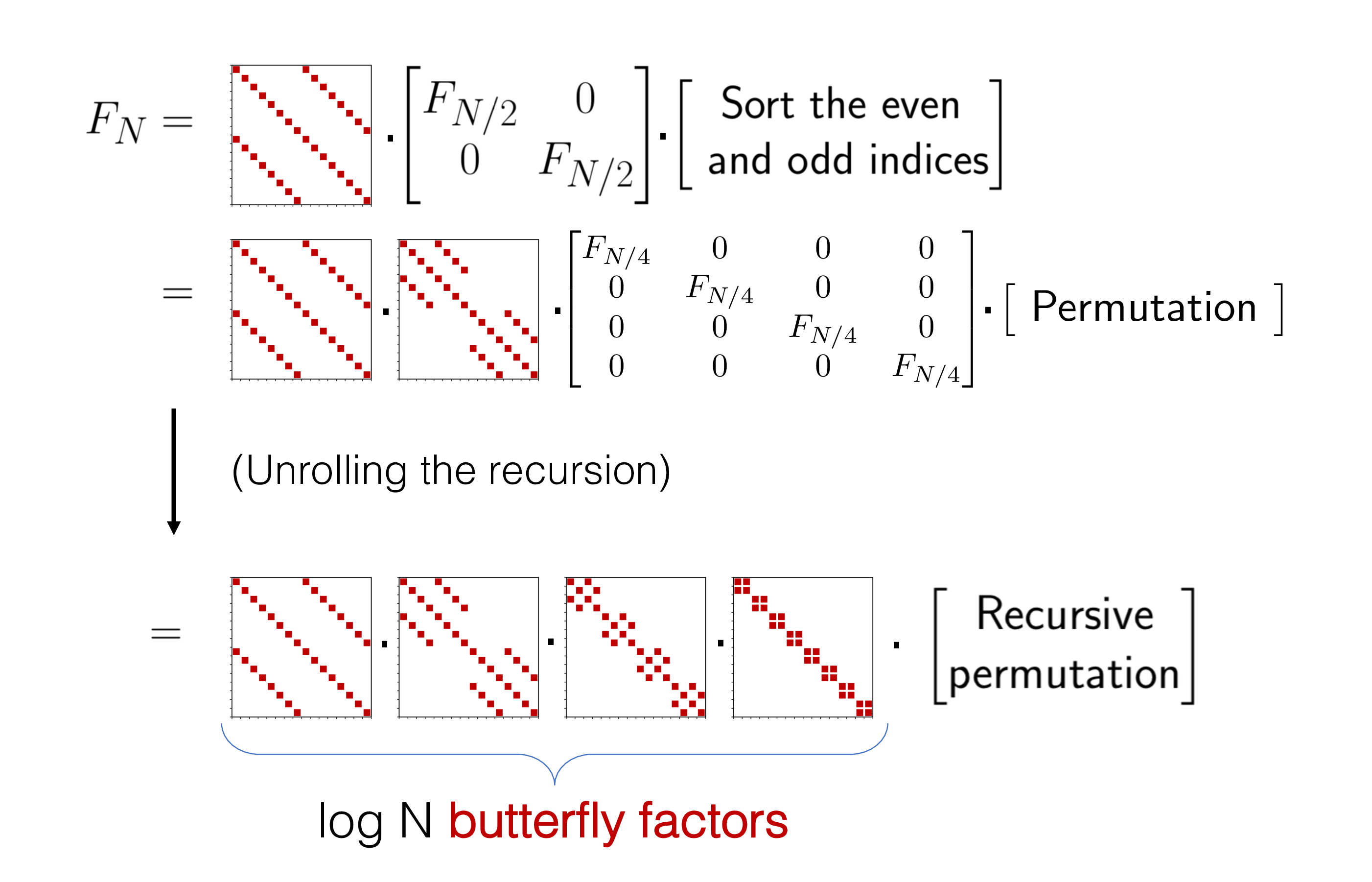
Butterflies Are All You Need A Universal Building Block For Structured Linear Maps Stanford Dawn

A Literature Survey Of Matrix Methods For Data Science Stoll 2020 Gamm Mitteilungen Wiley Online Library

Pin On Excel Tricks Tips Traps