Dot Product Matrix Multiplication Relationship
The dimensions involved in this multiplication are summarized in the following diagram. When taking the dot product of two matrices we multiply each element from the first matrix by its corresponding element in the second matrix and add up the results.
What Are The Conditions Necessary For Matrix Multiplication Quora
Y n H L L J x 1 y 1 x 2 y 2 x n y n.
Dot product matrix multiplication relationship. Dot product of 2-D vectors. Multiplication of two matrices involves dot products between rows of first matrix and columns of the second matrix. Let Abe a symmetric n nmatrix.
Let A be an m n matrix let B be an n p matrix and let C AB. Heres a picture of that for 2-D vectors. X n 3 5 Notice that quadratic forms are not linear transformations.
Ij is the result of taking the dot product of row i of matrix A and column j of matrix B. The dot product inner product of two vectors has the following properties. Thus one may define matrix--vector as.
The quadratic form associated to Ais the function Q A. Here is a diagram. Define a matrix and a matrix Compute the product.
C ij a i 1 b 1 j a i 2 b 2 j a in b nj. The fact that the dot product carries information about the angle between the two vectors is the basis of ourgeometricintuition. X y u v cosθ where θ is the angle between the vectors.
After that we talked about matrix multiplication where we actually invoke the dot product so with matrix multiplication you can only multiply two matrices if the number of columns in the first matches the number of rows in the second2070. In the special case where the matrix Ais a symmetric matrix we can also regard Aas de ning a quadratic form. They are different operations between different objects.
The first step is the dot product between the first row of A and the first column of B. If A is a square matrix and k is a positive integer we define Ak A AA k factors Properties of matrix multiplication. The dot product of two vectors x y in R n is x y G K K I x 1 x 2.
If we take two matrices and such that and then the dot product is given as Matrix Multiplication Two matrices can be multiplied together only when the number of columns of the first matrix is equal to the number of rows in the second matrix. The matrix product C AB denoted without multiplication signs or dots is defined to be the m p matrix C c 11 c 12 c 1 p c 21 c 22 c 2 p c m 1 c m 2 c m p displaystyle mathbf C beginpmatrixc_11c_12cdots c_1pc_21c_22cdots c_2pvdots vdots ddots vdots c_m1c_m2cdots c_mpendpmatrix. It is recommended that you explicitly use the multiplication operators between expressions that you wish to multiply.
Thinking of x y as column vectors this is the same as x T y. Define matrix--vector m v map lambda row dot-product v row m. Considertheformulain 2 againandfocusonthecos part.
Matrix multiplication does not commute in other words A times B does not equal B times A in general2084. Matrix multiplication is associative meaning that if A B and C are all n n matrices then ABC. Outer parameters become parameters of matrix AB What sizes of matrices can be multiplied together.
The connection between the two operations that comes to my mind is the following. The process taking place in Matrix Multiplication is taking the dot product of the transpose of a row vector in Matrix A dot its corresponding column vector in Matrix B. Matrix product is defined between two matrices.
341 Matrix-vector multiplication via dot product. The two are used interchangeably. Q Ax xAx is the dot product xTAx x 1 x n A 2 4 x 1.
The result of this dot product is the element of resulting matrix at position 00 ie. First row first column. A B row 1 colum1 x T y.
Then the ij entry of C is the i th row of A times the j th column of B. Thus is a matrix such that for each and the -th element of is equal to the dot product between the -th row of and the -th row of. Notice that multiplying a matrix to a vector is conceptually the same as obtaining the dot-product of the vector and each row of the matrix.
X n H L L J G K K I y 1 y 2. Finally the dot product can be thought of as a row vector or a 1 n matrix multiplied by a column vector an n 1 matrix. The row-column rule for matrix multiplication.
Matrix Multiplication is the dot Product for matrices. To calculate the c i j entry of the matrix C A B one takes the dot product of the i th row of the matrix A with the j th column of the matrix B. Of multiplication is not quite as straightforward and its properties are more complicated.
Matrix multiplication For m x n matrix A and n x p matrix B the matrix product AB is an m x p matrix. Dot product is defined between two vectors. V 1 a 1 a 2 a n v 2 b 1 b 2 b n v 1 v 2 a 1 b 1 a 2 b 2 a n b n.
Pin On Education Teaching Ideas
Matrix Multiplication And Linear Combinations
Matrix Multiplication Dimensions Article Khan Academy
Properties Of Matrix Scalar Multiplication Article Khan Academy
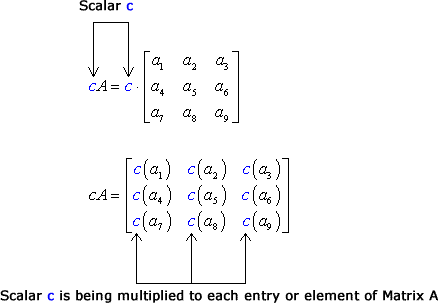
Scalar Multiplication Chilimath
How To Multiply Matrices Quick Easy Youtube
Matrix Multiplication In C Applying Transformations To Images
Introduction To Matrices And Matrix Arithmetic For Machine Learning
Multiplication Of 3x3 Matrices Matrix Multiplication Youtube
What Is The Relationship Between Matrix Multiplication And The Dot Product Quora
Matrix Matrix Multiplication Ml Wiki
Matrix Multiplication And Linear Combinations
Properties Of Matrix Multiplication Article Khan Academy
Pin On Matrices And Linear Systems High School Math Classroom Resources
Understand Dot Products Matrix Multiplications Usage In Deep Learning In Minutes Beginner Friendly Tutorial By Uniqtech Data Science Bootcamp Medium
