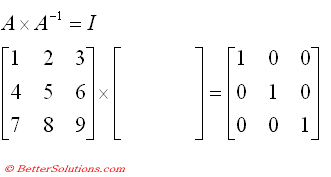Matrix Nonsingular Identity
All of its rows and columns are linearly independent. Ax 0has only the trivial solution x 0.

Why Can All Invertible Matrices Be Row Reduced To The Identity Matrix Mathematics Stack Exchange
Properties of non-singular matrix.
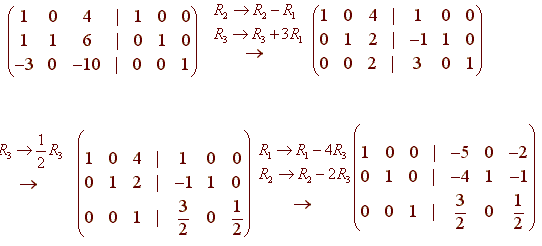
Matrix nonsingular identity. Theorem NMTNS Nonsingular Matrices have Trivial Null Spaces. Dina encoded a secret phrase using matrix multiplication. If A and B are non-singular matrices of the same order then AB is non-singular.
Suppose that A A is a square matrix. Nonsingular Matrices Row Reduce to the Identity. The multiplicative inverse of a square matrix is called its inverse matrix.
If a determinant of a square matrix is zero then only it is singular. An m m square matrix A of rank m is row equivalent to an identity matrix from the definition of reduced row echelon form. A square matrix A is said to be singular if A 0.
A non-singular matrix is a square one whose determinant is not zero. The identity matrix is the only idempotent matrix with non-zero determinant. If we suppose that P and Q are two 2 matrices of the order a x a satisfying the below condition-PQ I QP.
A matrix A is nonsingular if and only if A is invertible. Where I represents the Identity matrix whose order is a. That is it is the only matrix such that.
A has an inverse A-1such that AA-1 In. The principal square root of an identity matrix is itself and this is its only positive-definite square root. If A does not have an inverse A is called singular.
Prove that if either A or B is singular then so is C. If a matrix A has an inverse then A is said to be nonsingular or invertible. A square matrix is idempotent if A 2 A.
Thus a non-singular matrix is also known as a full rank matrix. We apply the elementary row operations as follows. Suppose that A A is a square matrix and B B is a row-equivalent matrix in reduced row-echelon form.
An n x n square matrix A is called non-singular if there exists an n x n matrix B such that AB BA In where In denotes the n x n identity matrix. We use the fact that a matrix is nonsingular if and only if it is row equivalent to the identity matrix. The next theorem pulls a lot of big ideas together.
Then A A is nonsingular if and only if the null space of A A is the set containing only the zero vector ie. 1 all non-zero rows are above rows of all zeros 2 the leading coefficient is strictly to the right of the leading coefficient of the row above 3 the leading coefficient is 1 and is the only non-zero number in its column. Here we are going to see how to check if the given matrix is singular or non singular.
A is row equivalent to the identity matrix In. She multiplied the clear text code for each letter by the matrix to get a matrix that represents the encoded text. C Show that if A is nonsingular then A is invertible.
Therefore the only nonsingular idempotent matrix is the identity. Add to solve later. By which matrix does Dina.
When multiplied by itself the result is itself. However every identity matrix with at least two rows and columns has an infinitude of. Then A A is nonsingular if and only if B B is the identity matrix.
N A 0 N A 0. To find the inverse of a square matrix A you need to find a matrix A 1 such that the product of. Which value of t makes the two matrices inverses of each other-3-2 2 3.
Identity matrix singular matrix non-singular matrix. An matrix A is nonsingular if and only if the reduced row echelon form of A is I the identity matrix. How to Identify If the Given Matrix is Singular or Nonsingular.
A square matrix A is said to be non-singular if A 0. A singular matrix does not have an inverse. B Let A B C be n n matrices such that AB C.
Multiplying by the inverse of A we get A I. The rank of a matrix A is equal to the order of the largest non-singular submatrix of A. It follows that a non-singular square matrix of n nhas a rank of n.
An n n matrix A is called nonsingular or invertible if there exists an n n matrix B such that AB BA I. A square matrix which is non-invertible is known as singular or degenerate. If the matrix is non-singular then its inverse exists.
Suppose A is nonsingular and idempotent. A Show that if A is invertible then A is nonsingular.

What Is An Inverse Identity Matrix Quora

What Is A Nonsingular Matrix Quora

The Inverse Of A Square Matrix A Is The Matrix A 1 Chegg Com
Https Web Northeastern Edu He Wang Teaching Teachingnotes Linearalgebra Section2 2 Pdf

I Is The Following Matrix Non Singular Ii Let C Chegg Com

How To Prove A Matrix Is Nonsingular In 10 Seconds Problems In Mathematics

Ex Determine If A 3x3 Matrix Is Invertible Nonsingular Using A Determinant Youtube

Why Can All Invertible Matrices Be Row Reduced To The Identity Matrix Mathematics Stack Exchange

If A Is Invertible Then It Can Be Represented As A Product Of Elementary Matrices Mathematics Stack Exchange

Confused About Elementary Matrices And Identity Matrices And Invertible Matrices Relationship Mathematics Stack Exchange

For Any Matrix A Show That There Are Non Singular Chegg Com

What Is An Inverse Matrix Mathbootcamps
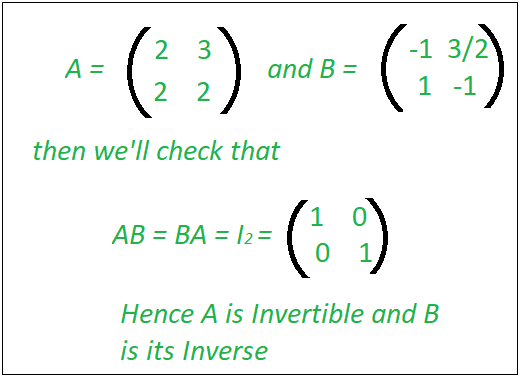
Check If A Matrix Is Invertible Geeksforgeeks

What Is An Inverse Matrix Mathbootcamps

2 10 Points Let A Be A Square Nonsingular Matrix Chegg Com