Show That G Is An Abelian Group Under Matrix Multiplication

10 Aug, 2021

Note that ab 1 b 1a 1 in general. 25Prove that a group G is Abelian if and only if ab 1 a 1b 1 for all a and b in G.

Properties Of Matrix Multiplication Article Khan Academy

Let G G L 2 R and H a 0 0 b.

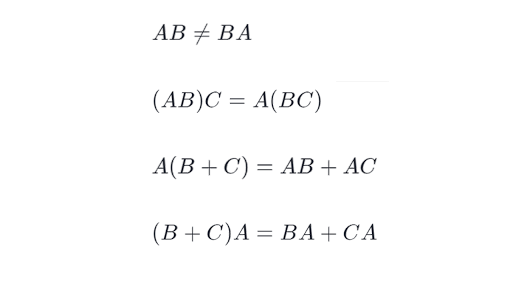
Show that g is an abelian group under matrix multiplication. Z Q R and C form inﬁnite abelian groups under addition. The required axioms matrix multiplication must satisfy to be a group operation the operation is not the whole group are. 3 Show that abH.

If XA X then also X XA 1. These are called trivial subgroups of G. More in Discrete Structures.

I will take it as known from linear algebra that matrix multiplication is associative. If the group is G g1 e g2 gn under the operation the i jth entry of thistable contains the product gi gj. Because G is Abelian b 1a 1 a 1b 1.

Every group Galways have Gitself and eas subgroups. Note that a 1b 1 ba 1. A and b are nonzero integers under the operation matrix multiplication.

Here are some basic. A group Gis Abelian or commutative if xy yxfor all elements xand yof G. Each element in G 0 is equal to e iθ for some θ R.

G- G 0 as follows. Write out the operation table for the gorup 2 X L. Therefore ab 1 ba 1.

N without zero is not a group under additionthere is no identity element. First if AB GLnR I know from linear algebra that detA 6 0 and det B 6 0. φ cos θ-sin θ sin θ cos θ e iθ.

The second list of examples above marked are non-Abelian. Associativity - For any three elements a b and c the equality a b c a b c must hold. Then G is a group if and only if for all ab G the equations ax b and ya b have solutions in G.

Show that GLnR is a group under matrix multiplication. We know at least that the function 1 exists for 2AutG since bijective is equivalent to invertible. These facts immediately imply that G is a subgroup of the group of invertible 2 2 -matrices.

N including zero is still not a group under addition since 3 has no additive inverse. Inverse - For every group element. φ is a bijective group homomorphism.

It is then straightforward to prove the following facts using only what you know about matrix multiplication. If the matrix is a symmetric matrix. It is given by the group presentation where e is the identity element and e commutes with the other elements of the group.

1 Show that eH where e is the identity 2 Assume that aH bH. Show that is an abelian group under matrix multiplication. Disprove that H is a subgroup of G G L 2 R.

In other words a group is Abelian if the order of multiplication does not matter. Each is an abelian monoid under multiplication but not a group since 0 has no multiplicative inverse. 1 What is the order of each group.

One usually adopts multiplicative notation for groups where the product xyof two elements x and yof a group Gis. It remains to show it is closed under inversion. Closuretotality any two elements of the group can be multiplied to get another element of the group associativity ident.

26Prove that in a group a 1 1 a. We observe that G A M2 2R det A 0 XA X. Identity element - There is a group element e the identity element such that a e e a a for any a in the group.

Show that 2x2 matrix G a b -b a ab in R not both 0 is an abelian group under matrix multiplication. To verify that a finite group is abelian a table matrix - known as a Cayley table - can be constructed in a similarfashion to a multiplication table. Define a map φ.

InnG is de ned as a subset of AutG so we need not show. De nition 7 Abelian group. In contrast the group of invertible matrices with a group law of matrix multiplication do not form an abelian group it is nonabelian because it is not generally true that M N N M MN NM M N N M for matrices M N MN M N.

This shows that AutG is a group. Is N a group under multiplication. I know multiplication of 2x2 matrices is always associative so this holds.

2 Show that G ab not both 0 is an abelian group under matrix multiplication. This proves that GLnR is closed under matrix multiplication. In group theory the quaternion group Q 8 sometimes just denoted by Q is a non-abelian group of order eight isomorphic to the eight-element subset of the quaternions under multiplication.

Solutions for Chapter 71 Problem 10E. Let G be a semigroup. Ab 1 a 1b 1 for all ab 2G G is Abelian.

Then detAB detAdetB 6 0. A group is Abelian4 if ab bafor all a 4 Also known as commutative bin G. Thus ab ab 1 1 ba 1 1 ba and G is Abelian.

Hence so AB GLnR. A group is abelian or commutative if for every ab G ab ba. The symmetric group S n S_n S n is also nonabelian for n 3 n geq 3 n 3.

Here the group operation on G is matrix multiplication and the group operation on G 0 is the multiplication of complex numbers. Thus AutG is closed under multiplication. 18 D 4 S 4 S 5 U 18.

Get solutions Get solutions Get solutions done loading Looking for the textbook. Well I have learned that I have to prove that. G is Abelian ab 1 a 1b 1 for all ab 2G.

The group is abelian if and only if this table is symmetric about the main diagonalie. Another presentation of Q 8 is. If we let ghbe in G then 1gh 1 g 1h 11 1g h since is a morphism 11g h meaning 1 is actually in AutG.

3 Consider the additive group 2 and the multiplicative group L 1 i of complex numbers.

Pin On Algebra