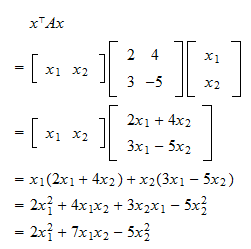Symmetric Matrices Positive Definite
Adaptive estimation and identification algorithms involving unknown symmetric and positive definite SPD matrix-valued parameters are ubiquitous in engineering applications. Also here I have some questions of my own.

Notation For The Set Of Symmetric Matrices And Symmetric Positive Definite Matrices Mathematics Stack Exchange
MIT 1806SC Linear Algebra Fall 2011View the complete course.

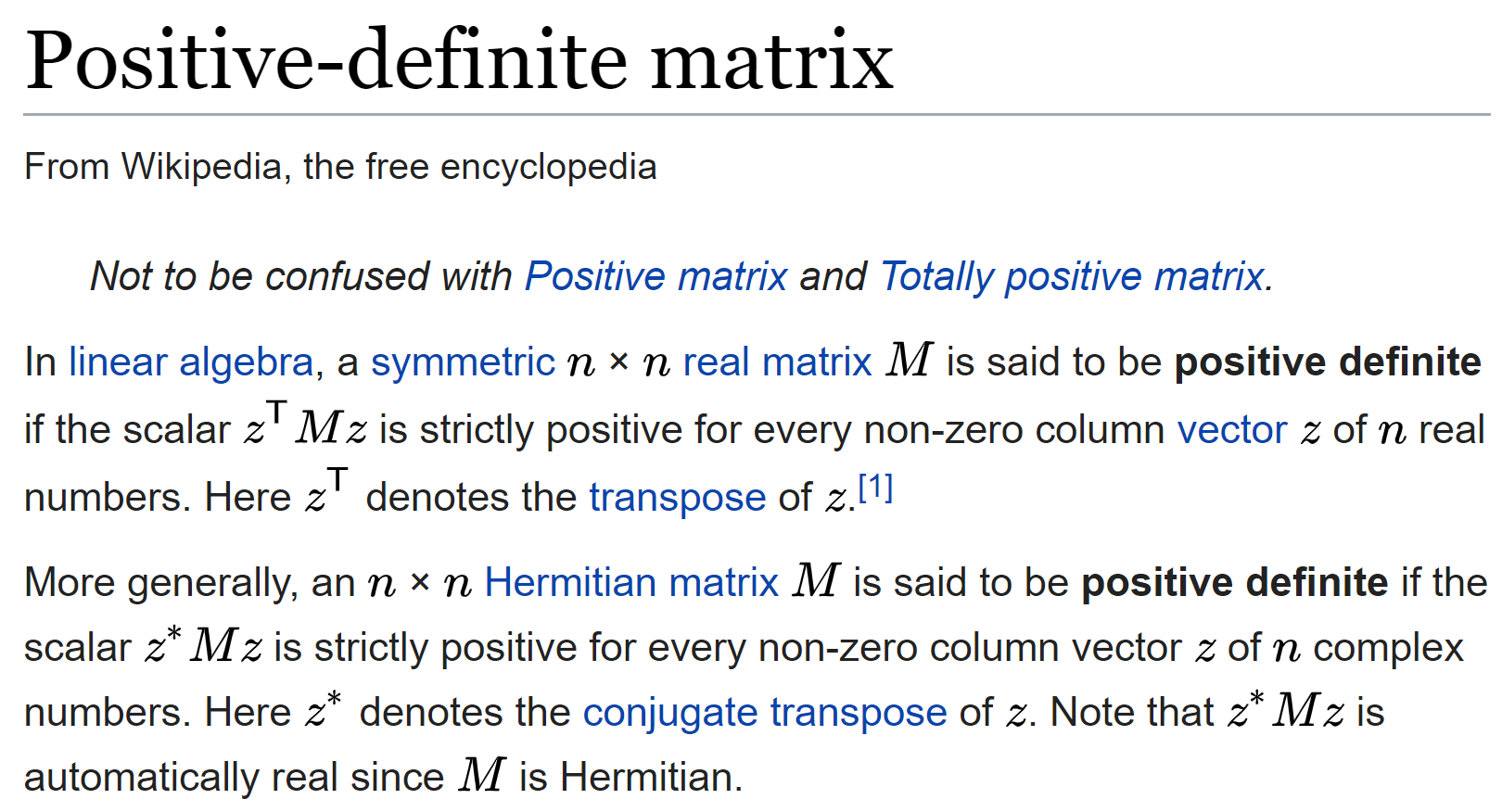
Symmetric matrices positive definite. I found out that there exist positive definite matrices that are non-symmetric and I know that symmetric positive definite matrices have positive eigenvalues. The problem of estimating the noise covariance matrices in estimation algorithms is considered first. The determinant of a positive definite matrix is always positive but the de terminant of 0 1 3 0.
Its eigenvalues are the solutions to. A Hermitian or symmetric matrix is positive definite iff all its eigenvalues are positive. B Consider a nonlinear system of the form.
Two examples pass and the third fails. Then is globally asymptotically stable. Then show that is globally asymptotically stable.
Therefore a general complex respectively real matrix is positive definite iff its Hermitian or symmetric part has all positive eigenvalues. Satisfies all the inequalities but for. A λI λ2 8λ 11 0 ie.
In this case xTAx AxTx. If every eigenvalue ofAis positive thenAis positive definite. 4 5.
All eigenvalues are positive. Satisfying these inequalities is not sufficient for positive definiteness. Œx1 x2 4 0 0 1 x1 x2 D4x2 1 Cx 2 2 0 Positive energy when x 0 Œx1 x2 5 4 4 5 x1 x2 D5x2 1 C8x1x2 C5x2 2 Positive energy when x 0 Œx1 x2 4 5 5 4.
Linear-algebra matrices eigenvalues-eigenvectors positive-definite. David ShirokoffA teaching assistant works through a. Positive definite implies x t A x 0 x 0.
Does this hold for non-symmetric matrices as well. MIT 1806 Linear Algebra Spring 2005Instructor. A real matrix is symmetric positive definite if it is symmetric is equal to its transpose and.
Because these matrices are symmetric the principal axes theorem plays a central role in the theory. Determinants of a symmetric matrix are positive the matrix is positive definite. Positive definiteness PD or semidefiniteness PSD requires the eigen values of the matrix either to be 0 or 0 respectively.
Example-Is the following matrix positive definite. Prove that if there exist two constant symmetric positive definite matrices such that. A Consider an autonomous nonlinear system of the form If there exist two constant symmetric positive definite matrices such that.
Let me test the energy xTSx in all three examples. Pivots are in general wayeasier to calculate than eigenvalues. A necessary condition in any quadratic programming to be convex is the matrix Q in the formulation x Q x to be positive definite or positive semidefinite.
Matrix is positive definite if its symmetric and all its pivots are positive. Definition A self-adjoint operator K acting on a Hilbert space H is called positive if hK f f i H 0 for. If v is an eigenvector of A then v t A v v t λ v λ 0 where λ is the eigenvalue associated with v.
For example the matrix. By making particular choices of in this definition we can derive the inequalities. Write the quadratic form for A as x t A x where superscript t denotes transpose.
Call the symmetric matrix A. The matrix is symmetric and its pivots and therefore eigenvalues are positive so A is a positive definite matrix. Positive Definite Matrices Kernels and Functions Positive Operators and Integrally PD Kernels In analogy to the positive semi-definiteness of a symmetric matrix we consider this notion for a self-adjoint operator Hoc73 Section 35.
A particularly important class of systems are the linear gradient flows in which AT is a symmetric positive definite matrix. LetAbe a real symmetric matrix. According to Theorem 823 all the eigenvalues of K are real and positive and so the eigenvalues of the negative definite.
Gilbert StrangView the complete course. 2 1 0 1 2 1 0 1 2 3 -L- L1 70 7 jcsive If x is an eigenvector of A then x 0 and Ax Ax. Positive Definite Matrices and the SVD 397 Positive energy is equivalent to positive eigenvalues when S is symmetric.
Inpractice this is usually the way youd like to do it. Justperform elimination and examine the diagonal terms. Positive Definite Matrices024811 A square matrix is called positive definite if it is symmetric and all its eigenvalues Math Processing Error are positive that is Math Processing Error.

Example Symmetric Positive Definite Matrix And Its Cholesky Factor Download Scientific Diagram

Determine If The 2x2 Matrix Is Positive Definite And Then Find The Cholesky Decomposition And An Ort Youtube

Note Set 23a Totally For Sure Positive Definite Matrices Matrixology
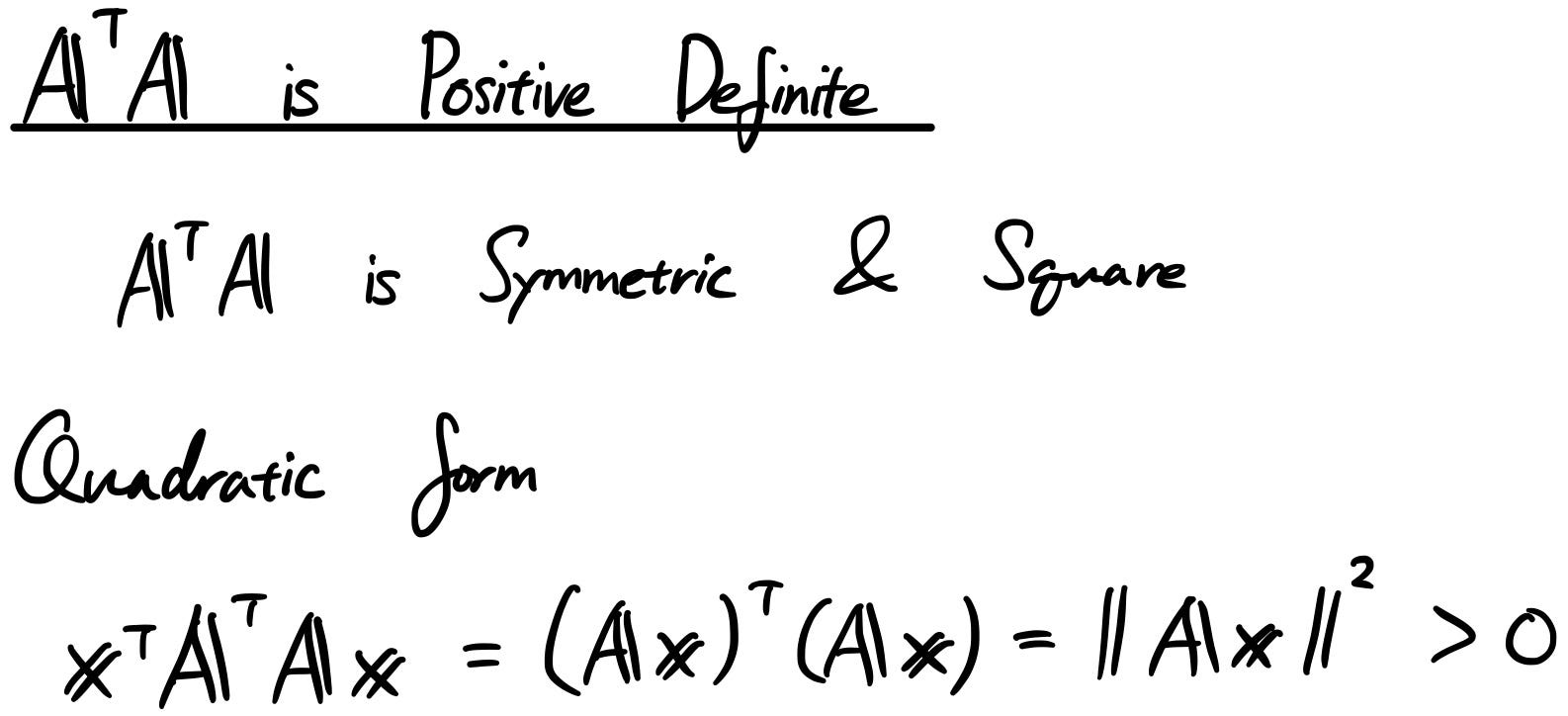
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium
Quadratic Forms And Positive Semidefinite Matrices Linear Algebra

Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Let A Be A Symmetric Positive Definite Matrix Show Chegg Com
What Is A Positive Definite Matrix By Aerin Kim Towards Data Science

Prove That Determinant Of A 2x2 Symmetric Positive Definite Matrix Is Positive By Completing The Square Method Mathematics Stack Exchange
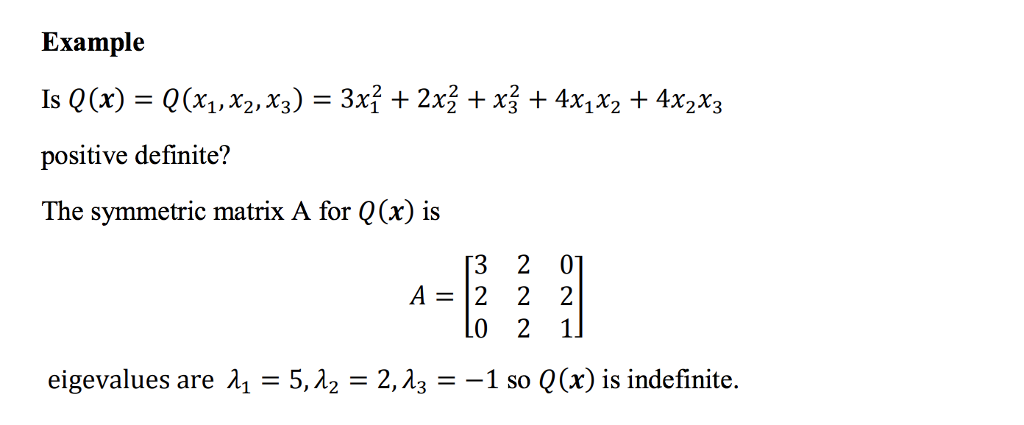
Example 7 3 Page 533 Let A Be A Symmetric Positive Chegg Com

Note Set 23a Totally For Sure Positive Definite Matrices Matrixology
Quadratic Forms And Positive Semidefinite Matrices Linear Algebra

Positive Definite Sequence And Its Corresponding Determinant Mathematics Stack Exchange

5 Positive Definite And Semidefinite Matrices Thevoltreport

The Symmetric Positive Definite Matrix A Product Of Chegg Com
How To Check If A Matrix Is Positive Definite Quora

Positive Definite Matrices Are Those Matrices For Chegg Com
Quadratic Forms And Positive Semidefinite Matrices Linear Algebra