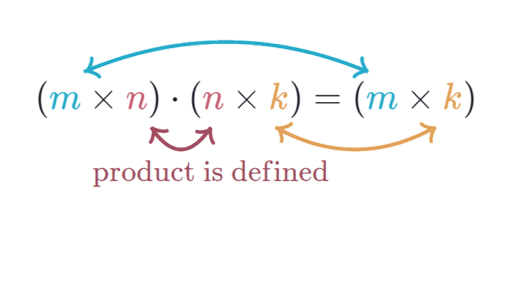Conventional Algorithm For Matrix Multiplication
Algorithm for Naive Method of Matrix Multiplication. Using this recurrence relation we get T n O n l o g 7 Hence the complexity of Strassens matrix multiplication algorithm is O n l o g 7.

2 9 Strassens Matrix Multiplication Youtube
Algorithm for Strassens matrix multiplication.

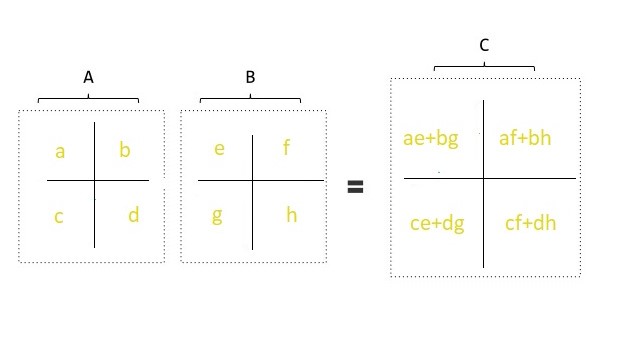
Conventional algorithm for matrix multiplication. Matrix C aebg afbh cedg cfdh. Given matrices A and B of size n we split each into 4 sub-matrices of size n2. Consider the following matrices A and B.
The fastest known matrix multiplication algorithm is Coppersmith-Winograd algorithm with a complexity of O n 23737. Strassens algorithm STRASSEN 1 for matrix-matrix multiplication DGEMM has fascinated theoreticians and prac- titioners alike since it was first published in 1969. Algorithm Strassenn a b d begin If n threshold then compute C a b is a conventional matrix.
Strassens algorithm Strassen 1 for matrix-matrix multiplication gemm has fascinated theoreticians and practitioners alike since it was rst published in 1969. 2 Calculate following values recursively. We compute the following seven products.
Matrix A a b matrix B e f c d g h There will be 8 recursive calls. Partition b into four sub matrices b11 b12 b21 b22. To compute C ij using this formula we need n multiplicationsAs the matrix C has n2 elementsthe time for the resulting matrix multiplication algorithmwhich we refer to as the conventional method is theta n3.
Why it needs three for loops. Tn 74 Tn. We denote A 1 1 A 1 2 A 2 1 A 2 2 as the sub-matrices of matrix A and B 1 1 B 1 2 B 2 1 B 2 2 as the sub-matrices of matrix B where A 1 2 denotes the sub-matrix on the top right of A.
That paper demonstrated that multiplication of n 3nmatrices can be achieved in less than the On arithmetic operations required by a. 9 rows In linear algebra the Strassen algorithm named after Volker Strassen is an algorithm for. Addition of two matrices takes O N 2 time.
Then Tn where psatisfies. 2 34 p 2. Theorem 31 memoryâcommunication tradeoff.
Strassens algorithm for matrix multiplication just gives a marginal improvement over the conventional ON3 algorithm. It has higher constant factors and is much harder to implement. I n On log 2 n and gn Onc if the function Tn satisfies the recurrence.
Square_matrix_multiplya b n arows let c be a new n x n matrix for i 1 to n for j 1 to n cij 0 for k1 to n cij cij aik bkj return c. We define Strassens algorithm as follows. For accessing all the elements of any matrix we need two for loops.
In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. The above strategy is. Matrix Multiplication Algorithm.
Given these shortcomings is strassens algorithm actually useful and is it. T n c i f n 1 7 x T n 2 d x n 2 o t h e r w i s e where c and d are constants. A e b g a f b h c e d g c f d h.
We then use these results to compute Cs submatricies. Start Declare variables and initialize necessary variables Enter the element of matrices by row wise using loops Check the number of rows and column of first and second matrices If number of rows of first matrix is equal to the number of columns of second matrix. Consider the conventional matrix multiplication C AB where A is m à n Bisn à r and C is m à r on a P-processor distributed-memory parallel computer with M words of local memory per processor.
The divide-and-conquer strategy suggests another way to compute the product of two n x. Previous Page Print Page. 1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram.
2 T34 n n2. Ae bg af bh ce dg and cf dh. Solvay Strassen algorithm achieves a complexity of O n 2807 by reducing the number of multiplications required for each 2x2 sub-matrix from 8 to 7.
Else Partition a into four sub matrices a11 a12 a21 a22.

Two Matrices Multiplication Using Mesh Algorithm Download Scientific Diagram
Numpy Matrix Multiplication Numpy V1 17 Manual Updated

Mapping Convolutions To Matrix Multiplication Operations Download Scientific Diagram
Matrix Multiplication Dimensions Article Khan Academy

Converting Convolution To Toeplitz Matrix Multiplication Convolution Download Scientific Diagram
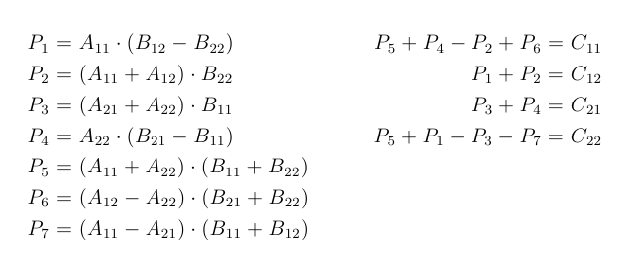
Strassen Matrix Multiplication C The Startup

Convolution Lowering Mapping A Convolution To A Matrix Matrix Download Scientific Diagram

Tuning Strassen S Matrix Multiplication For Memory Efficiency
Strassen S Matrix Multiplication Algorithm

Pseudocode For Matrix Multiplication Download Scientific Diagram
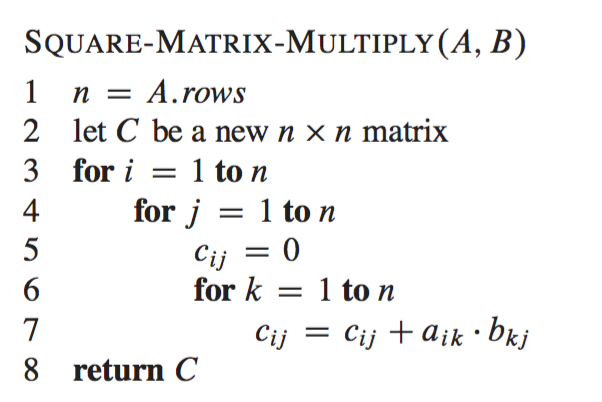
Matrix Multiplication Using The Divide And Conquer Paradigm

Matrix Multiplication In C Javatpoint

Wave Physics As An Analog Recurrent Neural Network Science Advances Physics Machine Learning Models Information Processing