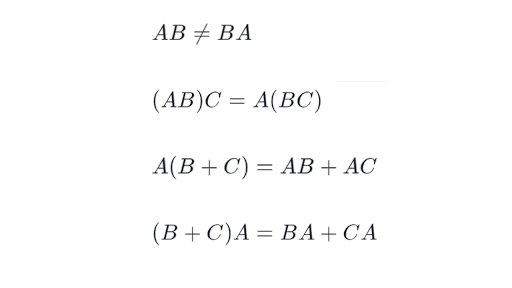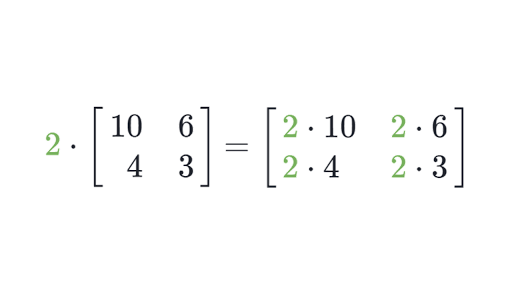Does Order Matter In Matrix Multiplication
Always keep in mind that for matrices AB almost certainly does. I would expect if these are the same that diff 0 and they should be the same since all I did was change the order of multiplying one term in the for loop at each iteration in the loop all terms are just numbers so there should be no difference in order.
A second way to control the order of operations is to change the matrix order argument.

Does order matter in matrix multiplication. The following example is the same as the preceding example except that Append has been changed to Prepend. Take matrix A row 1 is 1 2. Matrix multiplication is associative so ABC A BC ABC However multiplication is NOT commutative ie.
At the level of arithmetic the order matters because matrix multiplication involves combining the rows of the first matrix with the columns of the second. Matrix Multiplication - Order Matters. Does the order of matrix multiplication matter.
Well now the Law of Commutativity does matter because order does matter for matrix multiplication. The successive application of these matrices can act as complex transformations but because matrix multiplication is not commutative the order of these transformations matter. For instance 3X4 would be 3 rows of 4 columns.
That only saves operations if you are doing only one or two transformations. It doesnt matter which order you multiply the numbers in the result is the same. This video shows how to multiply three matrices when parentheses are present.
This does not work in general for matrices. Row 2 is 3 4 and matrix B row 1 is 8 7. Faulkner A question came up in our meeting today about the order of an array.
Yes it does matter. Matrix multiplication is not commutative so the order of arguments in each multiplication matters. The difference in the order is whether to multiply the vector first and have all the other matrixes multiply a vector reducing the number of operations since a vector is only 4x1 or multiply all the matrixes in order and only multiply the vector at the end.
Matrix multiplication is not commutative You know from grade school that the product 2 3 3 2. Diff sum sum l1-l2 I would expect if these are the same that diff 0 and they should be the same since all I did was change the order of multiplying one term in the for loop at each iteration in the loop all terms are just numbers so there should be no difference in order. The matrix multiplication is done in the order SRT.
Endgroup Abdullah Ali Sivas Dec 8 19 at 2328 begingroup It is indeed positive definite didnt think it was important so didnt mention it. Introducing you to those rules back then was probably kind of pointless since order didnt matter for anything you were multiplying then. Matrix multiplication is associative so you can multiply any adjacent pair of matrices first then multiply in the third one.
Our workbook that we have for our kiddos explicitly states that the first number in a multiplication equation is the number of rows and the second number is the number of columns. This path interpretation of matrix multiplication actually gets more intuitive for longer strings of matrixes because then each path consists of many steps. AB and BA do not give the same answer.
However it is pretty common to first scale the object then rotate it then translate it. Any combination of the order SRT gives a valid transformation matrix. If you swap the two matrices youre swapping which one contributes rows and which one contributes columns to the result.
I think if you take a larger indefinite matrix and it is possible that you will find a counter example. 1 yes the order does matter in how they represent the multiplication expression because as their illustrations show 56 is different that 65 when it comes to the situations described in the word problem. I see the question you pose 2 ways.
B x A 29. One way to reverse the order of individual transformations in a composite transformation is to reverse the order of a sequence of method calls. A x B 20.
L T R S If you do not do it in that order then a non-uniform scaling will be affected by the previous rotation making your object look skewed. In the last lesson we studied how matrices act on vectors stretches shrinkages reflections rotations etc and transform vectors into new vectors. For example each entry of a matrix product abcz is a sum over 26-step paths.
So you cant change the order in which you multiply any two of the three matrices in your formula. Each path visits 27 points but with just 26 transition-steps from one point to the next. Row 2 is 6 5.
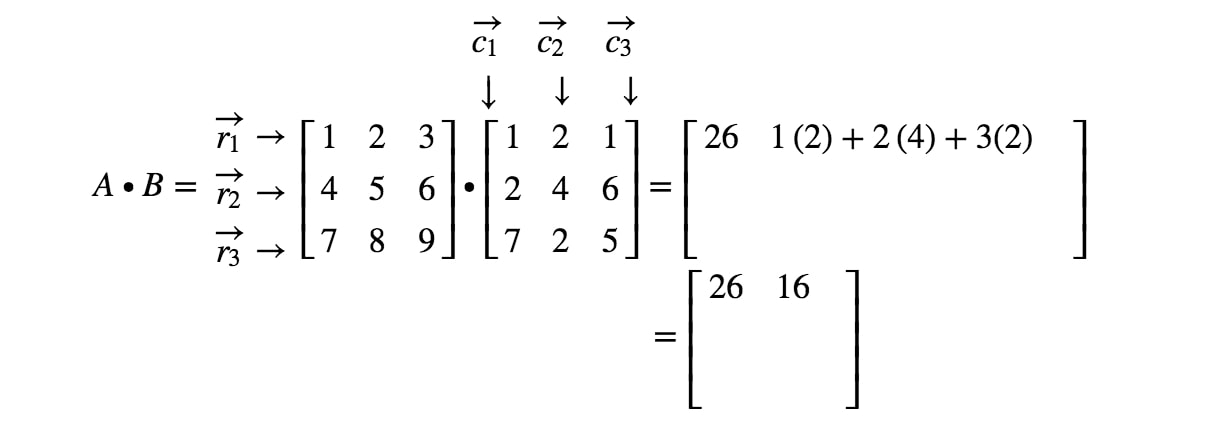
How To Multiply Two Matrices Together Studypug
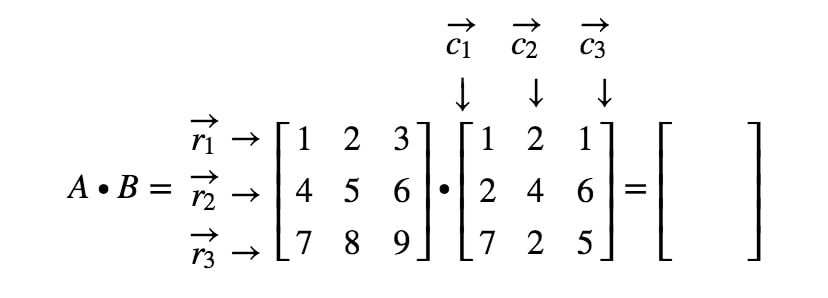
How To Multiply Two Matrices Together Studypug

How To Multiply Two Matrices Together Studypug
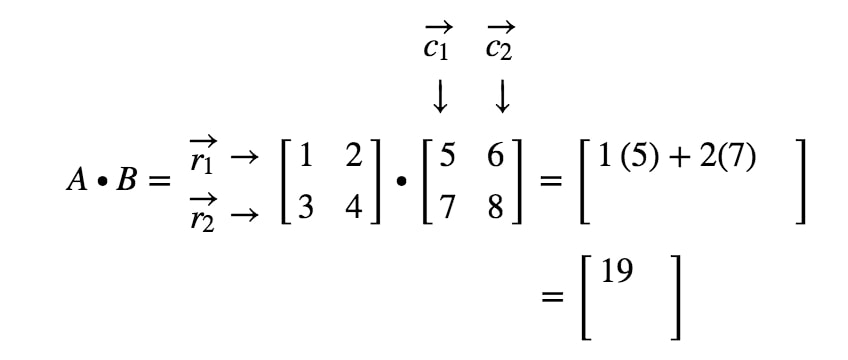
How To Multiply Two Matrices Together Studypug
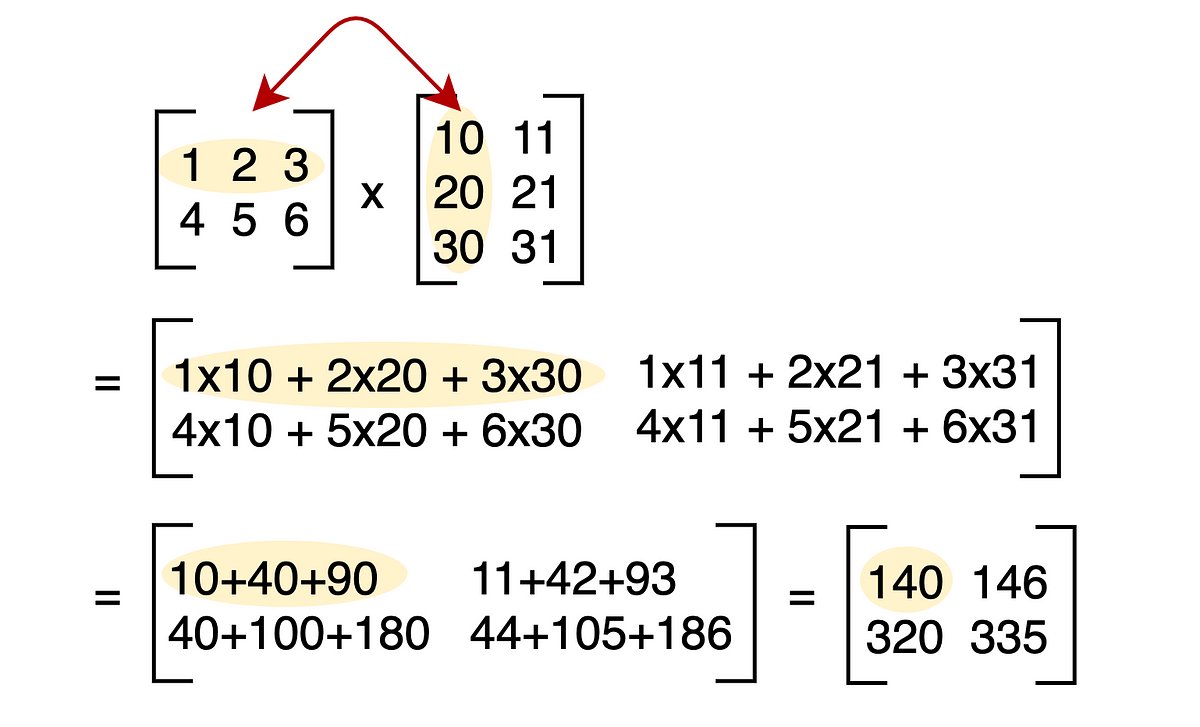
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science

3 4a Matrix Operations Finite Math
Properties Of Matrix Multiplication Article Khan Academy

How To Multiply Two Matrices Together Studypug

Question Video Determining Whether Matrix Multiplication Can Be Commutative Under Special Circumstances Nagwa
Matrix Multiplication Made Easy
Multiplying Matrices By Scalars Article Khan Academy
Matrix Multiplication Made Easy

Pin On Secondary Math And More
Matrix Multiplication Made Easy