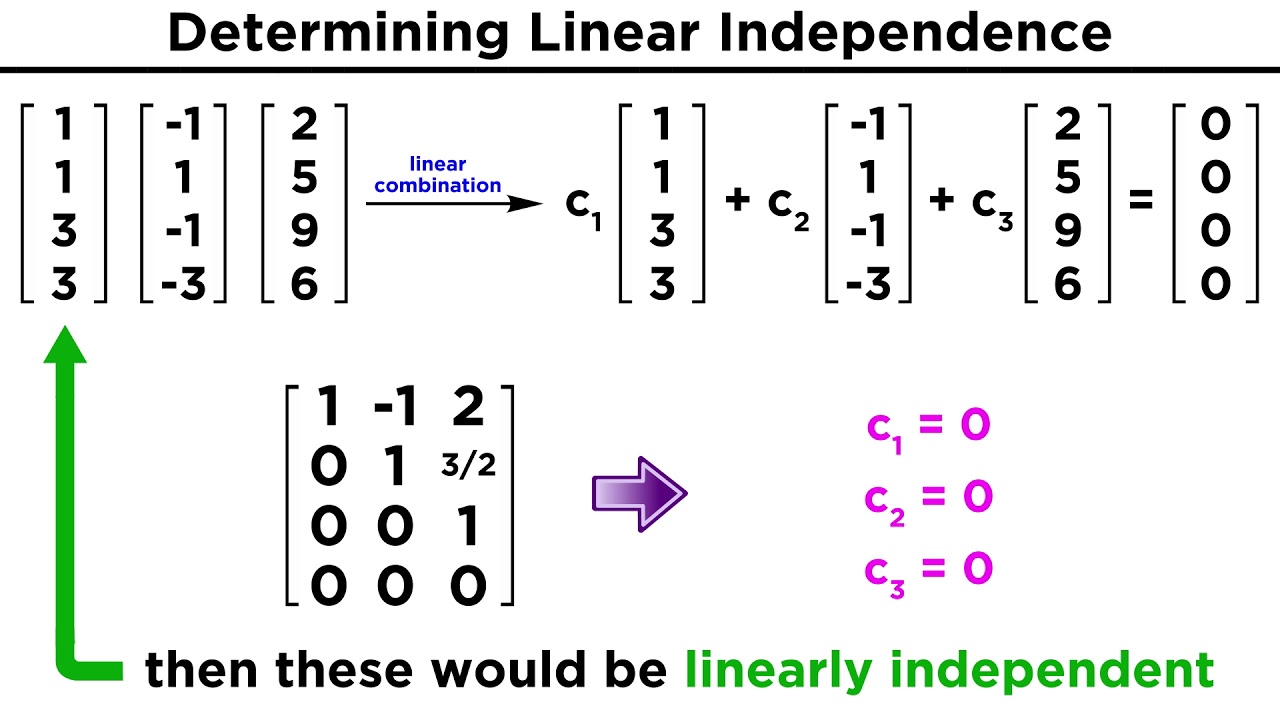
Matrices Columns Linearly Independent
0 c Find two 3 x 2 matrices A B where Az 0 has only the trivial solution and Be has an non-trivial solution. Then A cannot have a pivot in every column it has at most one pivot per row so its columns are automatically linearly dependent.

Linear Dependence And Independence Recall The Chegg Com
If no column row of a matrix can be written as linear combination of other columns rows then such collection of columns rows is called linearly independent.

Matrices columns linearly independent. For all values of. Given a set of vectors you can determine if they are linearly independent by writing the vectorsas the columns of the matrixA and solvingAx 0. Null and identity matrix E.
The dimension of the vector space is the maximum number of vectors in a linearly independent set. On the other hand a matrix that does not have these properties is called singular. We need to show that and In order to do this we subtract the first equation from the second giving.
Multiplication of matrices P AB. If there are any non-zero solutions then thevectors are linearly dependent. From numpy import dot zeros from numpylinalg import matrix_rank norm def find_li_vectorsdim R.
B Find a 4 x 7 matrix with linearly independent columns. Note that a tall matrix may or may not have linearly independent columns. A wide matrix a matrix with more columns than rows has linearly dependent columns.
A set of n vectors of length n is said to be linearly independent when the matrix with these vectors as columns has a non-zero determinant. Loop over the columns if i j. Does the conclusion hold if we do not assume that M has non-zero diagonal entries.
Basic matrix algebra 1. System of rows of square matrix are linearly independent if and only if the determinant of the matrix is not equal to zero. Matrices The array A ij.
6The rows of Aare linearly independent. A matrix A has linearly independent columns if and only if A has a trivial nullspace. Suppose and are two real numbers such that Take the first derivative of the above equation.
In the theory of vector spaces a set of vectors is said to be linearly independent when no vector in the set is a linear combination of the other. R matrix_rankR index zeros r this will save the positions of the li columns in the matrix counter 0 index0 0 without loss of generality we pick the first column as linearly independent j 0 therefore the second index is simply 0 for i in rangeRshape0. A v 1 2 2 3 3 pp0 is the trivial solution ai 0 for all i.
1 2 1 0 3 2 4 2 0 0 3 2 1 0 1 3 0 1 2 3 0 0 0 0 0 0. Linear independence via determinant evaluation. Now for your A note that.
Matrix addition and multiplication by a scalar 2. An A A_A 2. If the two columns.
5The columns of Aare linearly independent as vectors. In general AB 6 BA. A c 1 c n then the equation A x 0 is equivalent to.
The following are all equivalent. So for this example it is possible to have linear independent sets with. If Ahas these properties then it is called non-singular.
Choose the correct answer below. Facts about linear independence. If the only solution isx 0 then they are linearly independent.
Linear independence of functions. I have here three linear equations of four unknowns and like the first video where I talked about reduced row echelon form and solving systems of linear equations using augmented matrices at least my gut feeling says look I have fewer equations than variables so I probably wont be able to constrain this enough or maybe Ill have an infinite number of solutions but lets see if Im right so. For example four vectors in R 3 are automatically linearly dependent.
3pis linearly independent if the only solution to the equation av a v av. The columns of a matrix A are linearly independent if the equation Ax 0 has the trivial solution. Functions of matrices For a square matrix A the power is de ned.
X 1 c 1 x n c n 0. A set ofnvectorsinRn is linearly independent and therefore a basis if and only if it is theset of column vectors of a matrix with nonzero determinantTo verify this suppose the set of vectors isu1u2unand let uj u1ju2junj 1 j n. It is possible to have linearly independent sets with less vectors than the dimension.
Column Vectors of an Upper Triangular Matrix with Nonzero Diagonal Entries are Linearly IndependentSuppose M is an n times n upper-triangular matrix. If the diagonal entries of M are all non-zero then prove that the column vectors are linearly independent. The number of linearly independent rows or columns is equal to rank of the matrix.
ſi 1 d A number h so that the columns of 2 h 0 2 -1 5 are linearly independent. Let be the vector space of all differentiable functions of a real variable Then the functions and in are linearly independent. 1 vector or 2.
Theorem 3 Suppose Ais a square matrix. Given a set of column vectors they are linearly independent from each other only if solution of the null space formed by these column vectors is are zeroes otherwise they are linearly dependent. Vectors that are not linearly independent are called linearly dependent.
The way to determine this is to. The number of columns of A must be equal to the number of rows of B.

Sec 1 9 The Matrix Of A Linear Transformation Doc

In Each Part Determine Whether The Matrices Are Linearly Independent Or Dependent Mathematics Stack Exchange
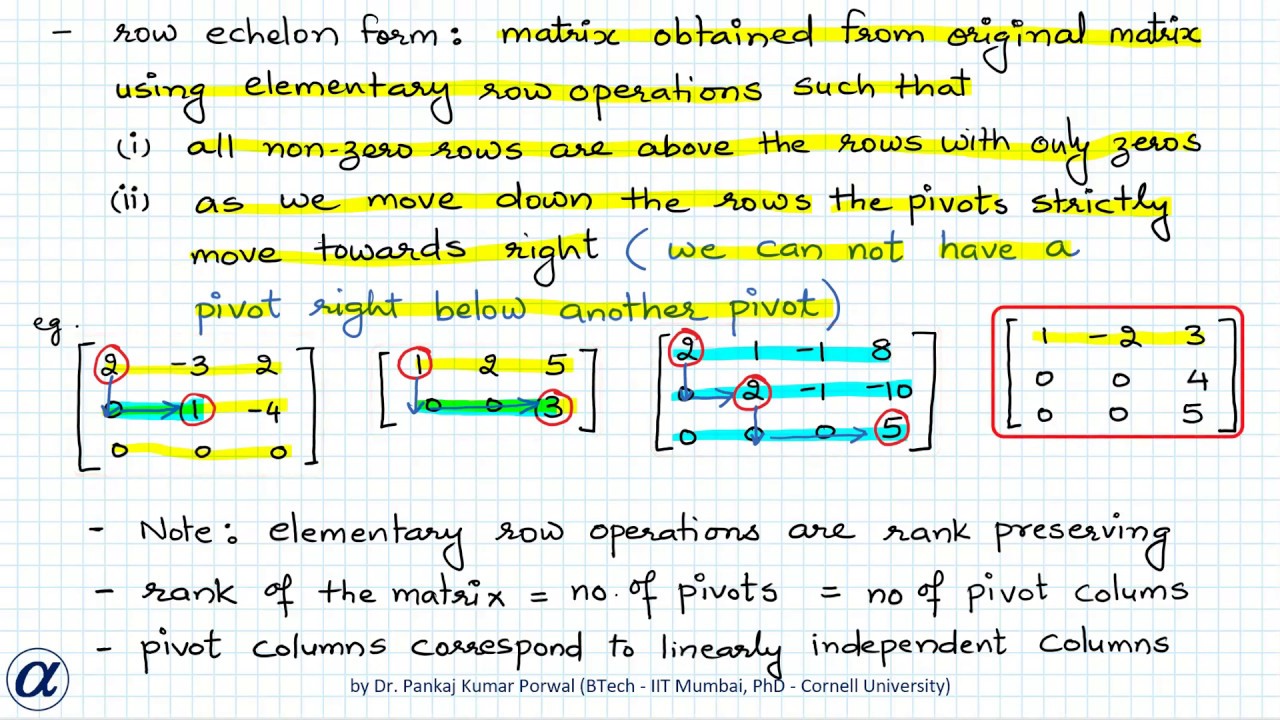
Rank Of A Matrix And Methods To Find The Rank Minor Method And Row Echelon Form Method Youtube

Verifying The Row Rank And Column Rank Of A Matrix Are Equal By Finding Bases For Each Mathematics Stack Exchange

What Is The Difference Between Linearly Independent And Linearly Dependent Quora
What Is The Difference Between Linearly Independent And Linearly Dependent Quora
Testing For Linear Dependence Of Vectors

Linear Algebra Example Problems One To One Linear Transformations Youtube

What Is The Difference Between Linearly Independent And Linearly Dependent Quora
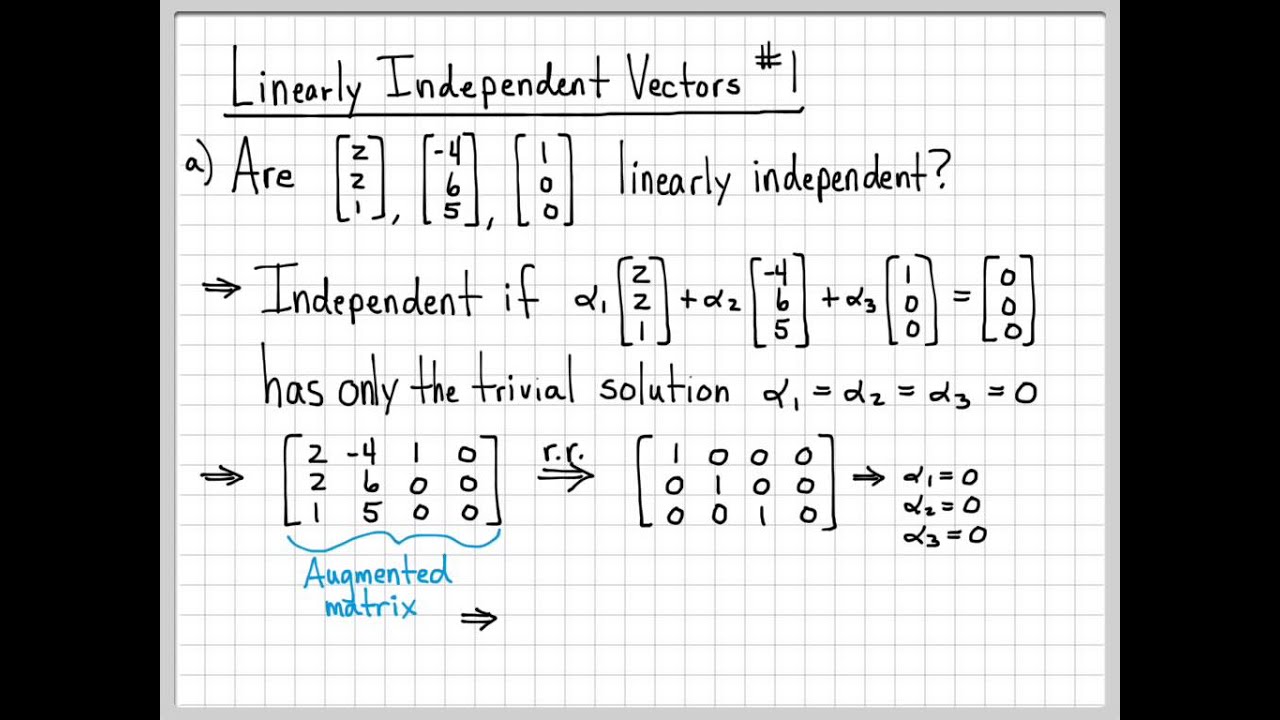
Linear Algebra Example Problems Linearly Independent Vectors 1 Youtube

Linear Algebra Example Problems Linearly Independent Vectors 1 Youtube