Matrix Chain Multiplication Quiz
Name the order of this matrix. Dp ij min dp ik dp k1j mat i-1mat kmat j.
Matrix Chain Multiplication Algorithm Javatpoint
26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30.

Matrix chain multiplication quiz. Initialize for k i to j 1 do try all possible splits costRec-Matrix-Chainp i. Out of all possible combinations the most efficient way is A BCD. Determine the dimensionsize of the new matrix.
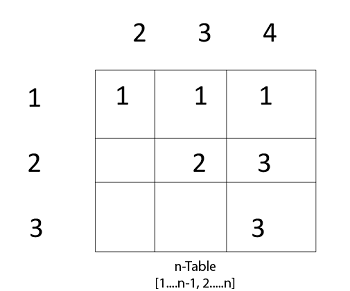
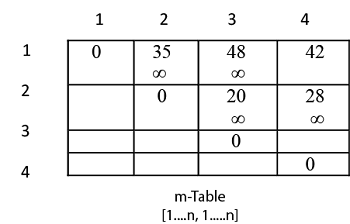
Count of multiplications for each parenthesis. N 4 arr 10 30 5 60 Output. N length p-1 Where n is the total number of elements And length p 5 n 5 - 1 4 n 4 Now we construct two tables m and s.
Int min IntegerMAX_VALUE. These matrices are being multiplied. Dp ij 0 if ij.
Each test case consists of an integer that denotes the value of n. Place parenthesis at different places between. No matter how one parenthesize the product the result will be the same.
Minimum-cost table m and split table s MATRIX-CHAIN-ORDER p n for i 1 to n m i i 0 for l 2 to n for i 1 to n-l 1 j i l-1 m i j for k i to j-1 q m i k m k 1 j p i-1 p k p j if q m i j m i j q s i j k return m and s Takes O n 3 time Requires O n 2 space. Dp ij min dp ik dp k1j mat i-1mat kmat j. Dijkstras SSSP algorithm.
Dimension of matrix Ai is pi - 1pi. The total number of multiplications are 123 134 145 6 12 20 38. Dp ij min dp ik dp k1j mat i-1mat kmat j.
Array p 0 n containing matrix dimensions and n Result. Matrix Chain Multiplication Consider the case multiplying these 4 matrices. The number of operations are - 203010 402010 401030 26000.
This set of Data Structure Multiple Choice Questions Answers MCQs focuses on Matrix-chain Multiplication. First and last matrix recursively calculate. To play this quiz please finish editing it.
You will be given an array p of size n 1. This quiz is incomplete. Length of array P number of elements in P length p 5 From step 3 Follow the steps in Algorithm in Sequence According to Step 1 of Algorithm Matrix-Chain-Order.
Find the product of the matrices. Placement and return the minimum count. That is determine how to parenthisize.
Longest increasing subsequence. P 40 20 30 10 30 Output. ABCD - This is a 2x2 multiplied by a 2x1.
Let n optdimshigh optm newSeqWithn newSeqNaturaln opts newSeqWithn newSeqNaturaln for lg in 1. You need to find minimum number of multiplications needed to multiply the chain. The matrices have dimensions 1030 305 560.
If i j return 0. Consider the two matrices P and Q which are 10 x 20 and 20 x 30 matrices respectively. Let the input 4 matrices be A B C and D.
Find the product of the two matrices. 11-13 Algorithm to Compute Optimal Cost Input. For i in 0.
The first line contains a single integer T representing the number of test cases. Find the product of the matrices. Consider the two matrices P and Q which are 10 x 20 and 20 x 30 matrices respectively.
ABCD Explaination. The Chain Matrix Multiplication Problem Given dimensions corresponding to matr 5 5 5 ix sequence 5 5 5 where has dimension determinethe multiplicationsequencethat minimizes the number of scalar multiplications in computing. Static int MatrixChainOrder int p int i int j.
We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain. Find the best order for matrix chain multiplication. Consider the two matrices P and Q which are 10 x 20 and 20 x 30 matrices respectively.
Here Chain means one matrixs column is equal to the second matrix. Dp ij min dp ik dp k1j mat i-1mat kmat j. ABCD - This is a 2x4 multiplied by a 4x1 so 2x4x1 8 multiplications plus whatever work it will take to multiply BCD.
Rec-Matrix-Chainarray p int i int j if i j mi i 0. Dp ij 0 if ij. It is a Method under Dynamic Programming in which previous output is taken as input for next.
The recurrence relation is given by. Basic case else mi j infinity. You can multiply a 6X2 matrix by which matrix.
Say the matrices are named as A B C D. There are many options to multiply a chain of matrices because matrix multiplication is associative ie. In this video on dynamic programming I have discussed about matrix chain multiplication problem which is based upon dynamic programmingPractice questions.
N 5 p 1 2 3 4 5 Output. The recurrence relation is given by. Detecting bipartiteness 2-colorability Depth-first search.

More Dynamic Programming Matrix Chain Multiplication Announcements I

Matrix Chain Multiplication Geeksforgeeks Youtube

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication Docsity

Ppt Matrix Chain Multiplication Powerpoint Presentation Free Download Id 444060

Lecture 13 Dynamic Programming Steps The Seven Steps
Cs 570 Analysis Of Algorithms Spring 2012

Solved Algorithms Uiz 2013 12 25 1 20 1 10 Matrix Chain Multiplication Problem Stated Follows Giv Q38201803

Ppt Dynamic Programming Powerpoint Presentation Free Download Id 3687377

Lecture 13 Dynamic Programming Steps The Seven Steps
Matrix Multiplication Gate Overflow

Ppt Matrix Chain Multiplication Powerpoint Presentation Free Download Id 444060
Matrix Chain Multiplication Algorithm Javatpoint

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube

More Dynamic Programming Matrix Chain Multiplication Announcements I
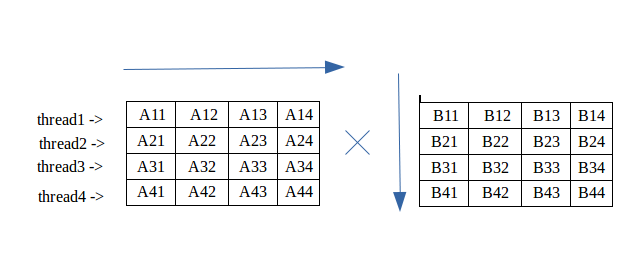
Multiplication Of Matrix Using Threads Geeksforgeeks
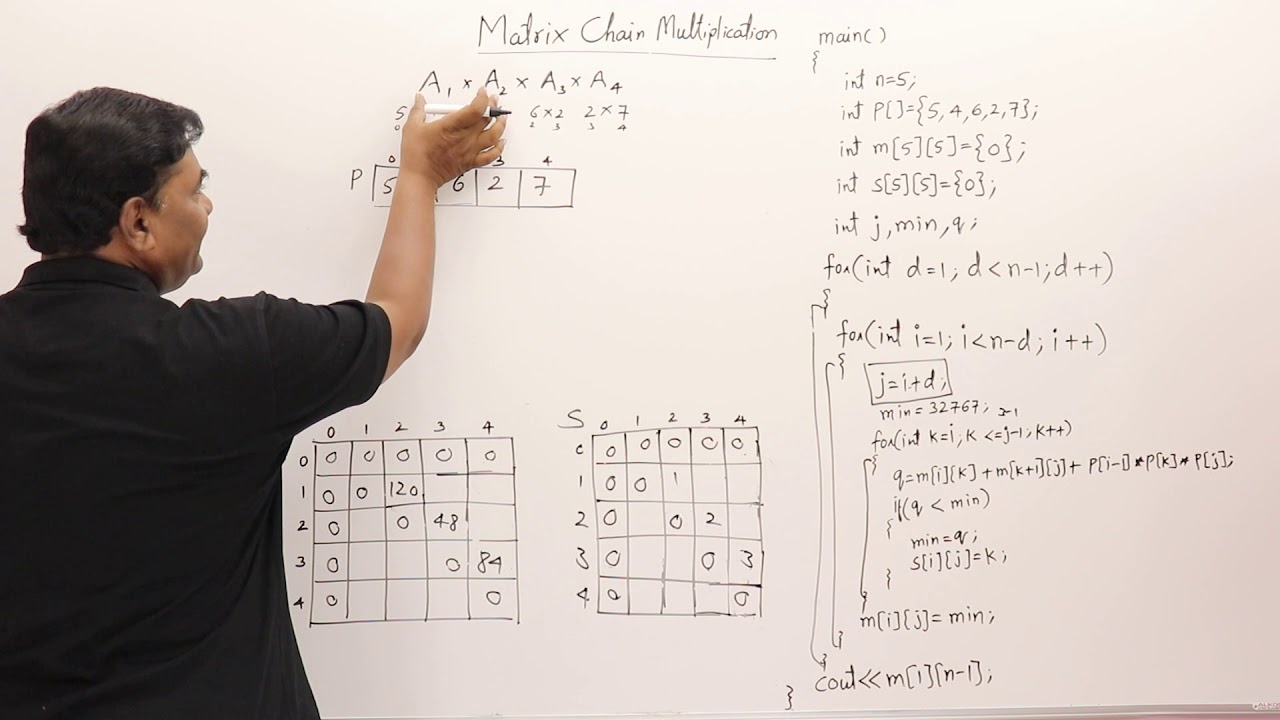
4 3 Matrix Chain Multiplication Dynamic Programming Youtube