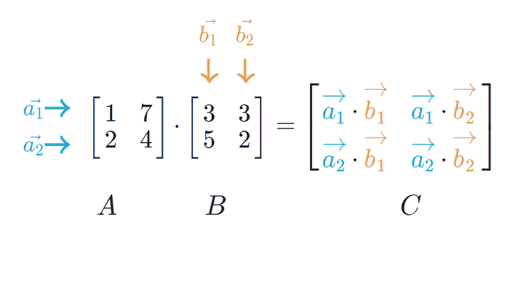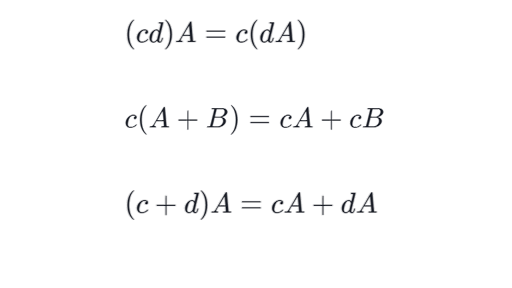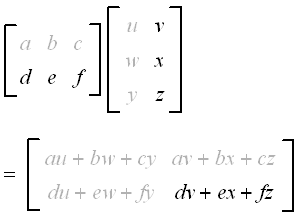Matrix Cross Product Rules
The dot product will result in cos 01 and the multiplication of the vector lengths whereas the cross product will produce sin 00. Recall that the determinant of a 2x2 matrix is and the determinant of a 3x3 matrix is Notice that we may now write the formula for the cross product.
Description If A and B are vectors then they must have a length of 3.
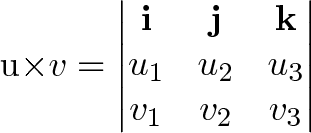
Matrix cross product rules. The cross product is defined to be the one of these two vectors where the motion from the tip of the first input vector to the tip of the second input vector is in a counter-clockwise direction when observed from the side of the normal. By the right-hand rule it must be j. Electricity and magnetism relate to each other via the cross product as well.
Taking for example two parallel vectors. There are lots of other examples in physics though. As with the dot product the cross product of two vectors contains valuable information about the two vectors themselves.
The one way that we know to get an orthogonal vector is to take a cross product. Two vectors have the same sense of direction. If latexAlatex is an latextext mtext times text rtext latex matrix and latexBlatex is an latextext rtext times text ntext latex matrix then the product matrix latexABlatex is an.
This is just a restatement of the right-hand rule that you are familiar with. If you want to go farther in math you should know the matrix bit of. Like the dot product the cross product behaves a lot like regular number multiplicationwith the exceptionof property1.
It again results in a vector which is perpendicular to both the vectors. Finding the product of two matrices is only possible when the inner dimensions are the same meaning that the number of columns of the first matrix is equal to the number of rows of the second matrix. Although this may seem like a.
Cross product is the binary operation on two vectors in three dimensional space. Finally the cross product of any vector with itself is the zero vector a a 0. The cross product is linear in each factor so we have for example for vectors x y u v ax by cu dv acxu adxv bcy u bdy v.
If a plane contains the points P left 100 right Q left 111 right and R left 2 - 13 right find a vector that is orthogonal to the plane. For the cross product by using the properties of determinants. The cross product distributes across vector addition just like the dotproduct.
The cross product of two parallel vectors is 0 and the magnitude of the cross product of two vectors is at its maximum when the two vectors are perpendicular. The cross product isnot commutative. The cross product of two vectors are zero vectors if both the vectors are parallel or opposite to each other.
Cross product of two vectors is calculated by right hand rule. Right hand rule is nothing but the resultant of. The other type called the cross product is a vector product since it yields another vector rather than a scalar.
With the two kinds of multiplication of vectos the projection of one to the other is included. This is my easy matrix-free method for finding the cross product between two vectors. J i k k j i i k j.
In this case the cross. If A and B are matrices or multidimensional arrays then they must have the same size. Conversely if two vectors are parallel or opposite to each other then their product is a zero vector.
By remembering that b a a b you can infer that. θ 90 degrees. In particular the cross product of any standard unit vector with itself is the zero vector.
As we know sin 0.
Multiplying Matrices Article Matrices Khan Academy
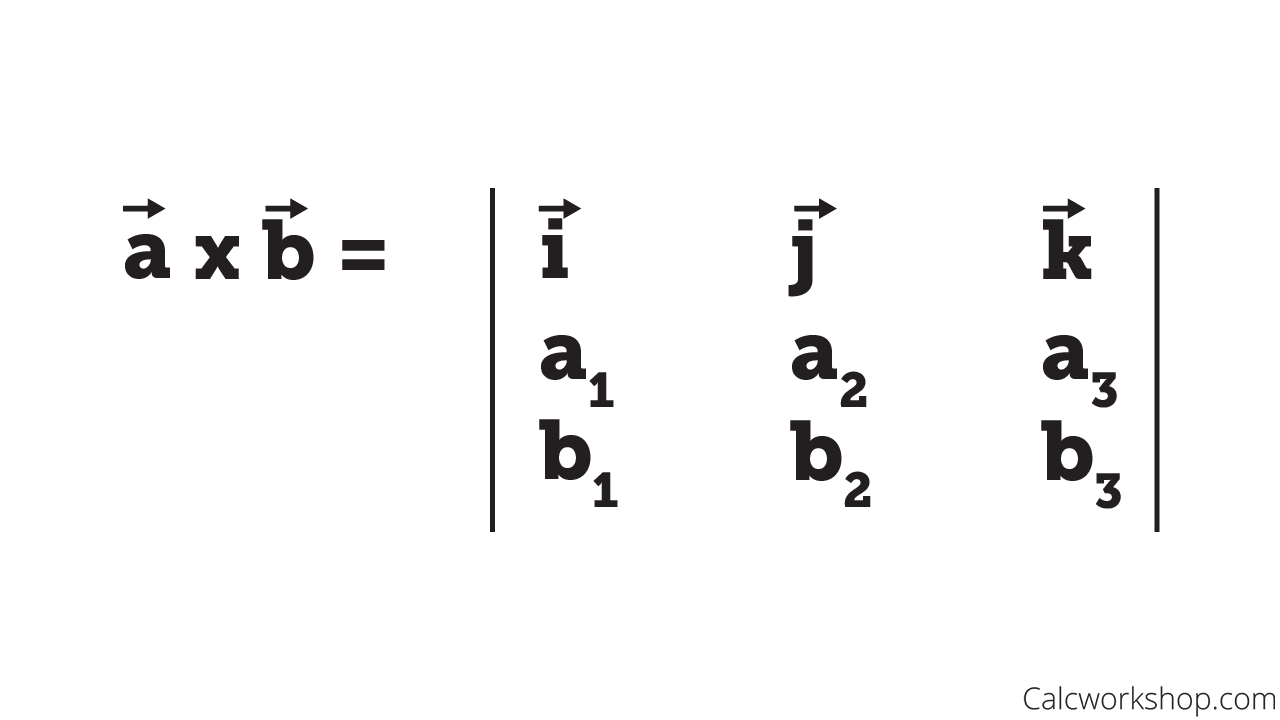
Cross Product For Calculus Everything You Need To Know
Properties Of Matrix Scalar Multiplication Article Khan Academy

Product Of Vectors Vector Can Vector Multiplication
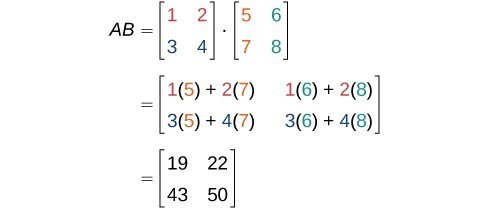
Finding The Product Of Two Matrices College Algebra
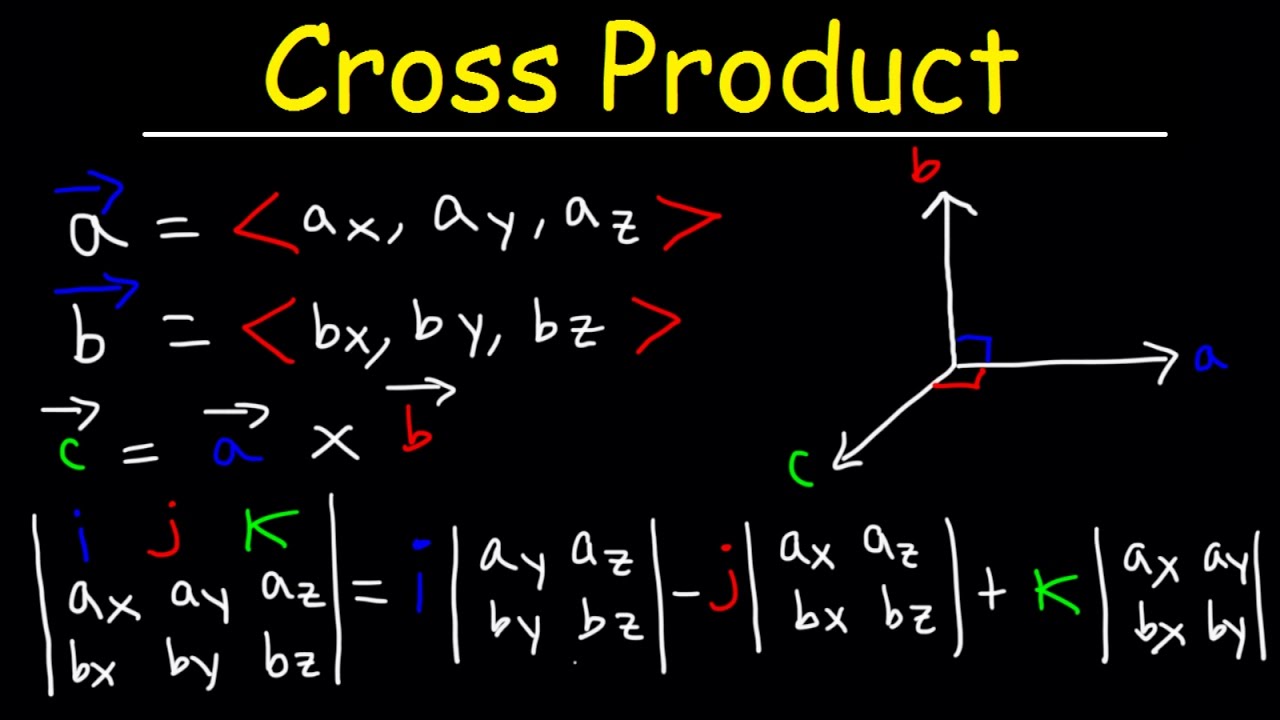
Cross Product Of Two Vectors Explained Youtube
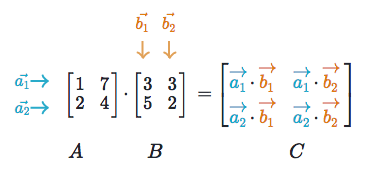
Linear Algebra Ml Glossary Documentation
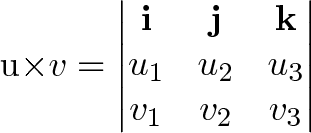
Vector Calculus Understanding The Cross Product Betterexplained

How To Calculate Cross Product Matrix Youtube

Intro To Matrices Youtube Matrix Intro Precalculus

Cross Product For Calculus Everything You Need To Know