Scalar Vector And Matrix Mathematics Pdf
Multiply a vector by a scalar. Perform scalar multiplication component-wise eg as cv x v y cv x.
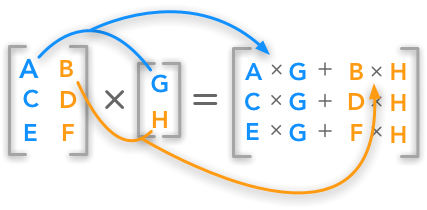
Introduction To Matrices And Vectors Multiplication Using Python Numpy
And when we include matrices we get this interesting pattern.
Scalar vector and matrix mathematics pdf. The Dot Product The result of a dot product of two vectors is a scalar. In particular and are opposite vectors. Then the vector from the terminal point of v to the terminal point of u is the vector u v.
1Associativity of vector addition. But kA Ak if k is a scalar and A is a matrix. An operation called scalar multiplication that takes a scalar c2F and a vector v2V and produces a new vector written cv2V.
Ax2y242325 The magnitude of a vector is a scalar value a number representing the length of the vector independent of the direction. Other notation for C AB c ij n k1 a ikb kj 1 i m 1 j p. Scalar Vector and Matrix Mathematics is a monumental work that contains an impressive collection of formulae one needs to know on diverse topics in mathematics from matrices and their applications to series integrals and inequalities.
Let A 101 321 and B 21 30 11. Ii position u and v so that their initial points coincide. JIncludes bibliographical references and index.
Princeton University Press 2018 jRevised and expanded edition of Matrix mathematics retitled Scalar vector and matrix mathematicsPreface. Vector we can use the Pythagorean theorem x2y2z2. Which satisfy the following conditions called axioms.
For any mn matrix A AI A. The scalar multiplication of a vector satisfies the distributive laws. 2Existence of a zero vector.
The nn matrix I whose jth column is the jth unit vector is called an identity matrix. The bibliography is vast and well documented and the presentation is appealing and accessibleOvidiu. Represent scalar multiplication graphically by scaling vectors and possibly reversing their direction.
We denote matrix multiplication with a scalar by placing the scalar and the matrix side by side usually with the scalar on the left. There are a lot of examples were the magnitudes of vectors are important to us. BAIn generalAB.
INTRODUCTION In this appendix we outline the notation that we use in this book and then some of the mathematics of matrices and closely related vectorsThis material is worth mastering because notation is important in ensuring consistency in many of the materials we present and as will be. Its only nonzero entries are the diagonal entries 1. I ii Multiplying a vector by a scalar If v is a nonzero vector and c is a nonzero scalar we define the product of c and v.
For example U 1 X t U 1 x 1xn x 1. The product C AB is the mp matrix defined by c ij r iAc jBX where r iA is the vector in R n consisting of the ith row of A and similarly c jB is the vector formed from the jth column of B. Mn a mn a nm a 2.
When first published in 2005Matrix Mathematicsquickly became the essential reference book for users of matrices in all branches of engineering science and applied mathematicsIn this fully updated and expanded edition the author brings together the latest results on matrix theory to make this the most complete current and easy-to-use book on matrices. For any mn matrix A AUj is the jth column of A. In fact a vector is also a matrix.
Clearly I t I. Scalars Vectors and Matrices. According as K is positive or negative resp.
The bibliography is vast and well documented and the presentation is appealing and accessibleOvidiu. And AI IA if A is a matrix and I is the identity matrix. No multiplication symbol is necessary.
Revised and expanded edition. Vector and Matrix Quantities Secondary I Honors Core Content Cluster Title. Because a matrix can have just one row.
Properties of Multiplication of Vectors by Scalars. Jth column of AI A jth column of I. A m x 1 column vector multiplied by a 1 x n row vector becomes an m x n matrix.
Notation Matrices and Matrix Mathematics A1. There is a vector in V written 0 and called. The scalar multiplication of a vectors satisfies.
Then AB 12 11 4. 715 Multiplying a Matrix with a Scalar A matrix M may be multiplied with a scalar k resulting in a matrix of the same dimension as M. Perform operations on vectors.
AU 1. The Dot Product F 2iˆ3ˆj2kˆN r s 3iˆ 4ˆj6kˆ m r F s rr 23Nm 34Nm26Nm. AB ABcosθ r r A r B r θ ˆ ˆ 1 ˆ ˆ 1 ˆ ˆ 1 k k j j i i ˆ ˆ 0 ˆ ˆ 0 ˆ ˆ 0 i k j k i j Vector Multiplication I.
MatrixEquation an a a xn x scalars vector equations x ait xaz scalarmultiples of aes matrixequations Amin. The essential reference book on matrices-now fully updated and expanded with new material on scalar and vector mathematics. Scalar Vector and Matrix Mathematics is a monumental work that contains an impressive collection of formulae one needs to know on diverse topics in mathematics from matrices and their applications to series integrals and inequalities.
Since its initial publication this book has become the essential reference for users of matrices in all branches of engineering science and applied mathematics. Matrix Equationpdf from MATH 2B at Foothill College. A 1 x m row vector multiplied by a m x 1 column vector becomes a scalar.
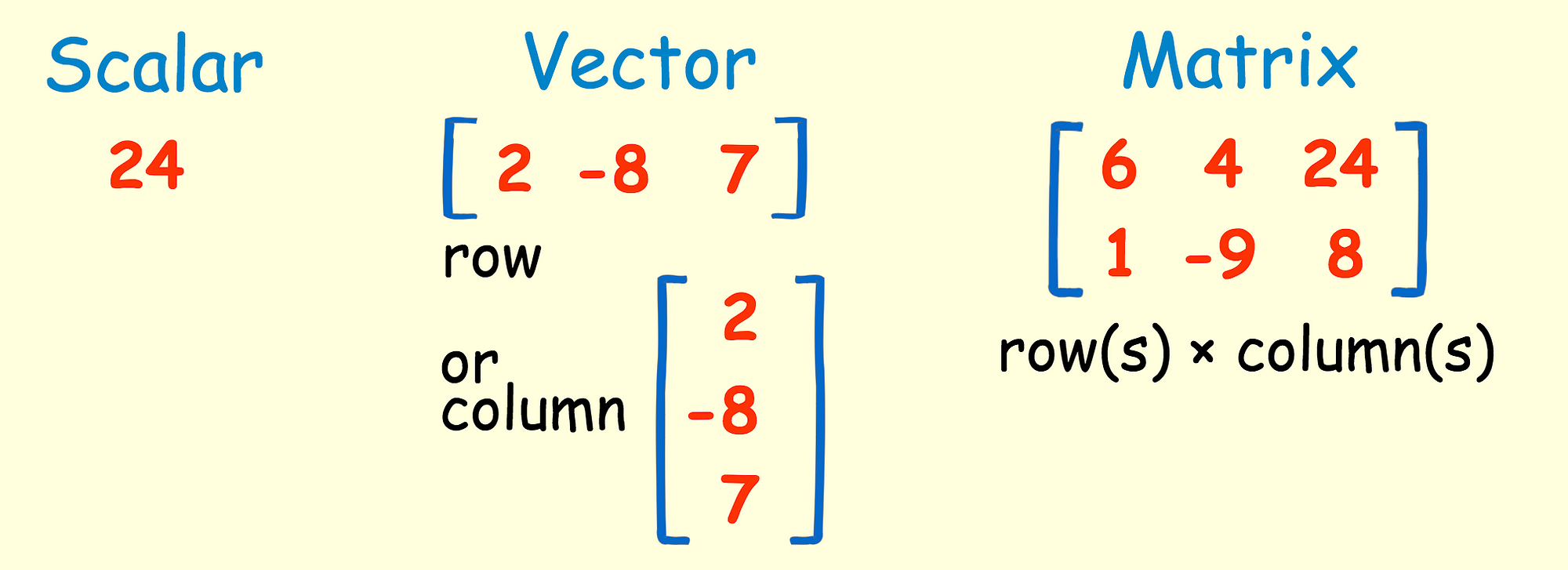
Direction is that of vector or opposite to vector. U v w u v w for all uvw2V. A scalar is a number like 3 -5 0368 etc A vector is a list of numbers can be in a row or column A matrix is an array of numbers one or more rows one or more columns.

Introduction To Vectors And Matrices Using Python For Data Science Data Science Learning Mathematics Math Formulas

How Mathematics Happened The First 50 000 Years By Peter Strom Rudman Math Books Mathematics Math Brainteasers

Scalar Vector And Matrix Mathematics Princeton University Press

Fundamentals Of Matrix Algebra Open Textbook Library

Basic Linear Algebra For Deep Learning By Niklas Donges Towards Data Science

Matrix Mathematics Princeton University Press
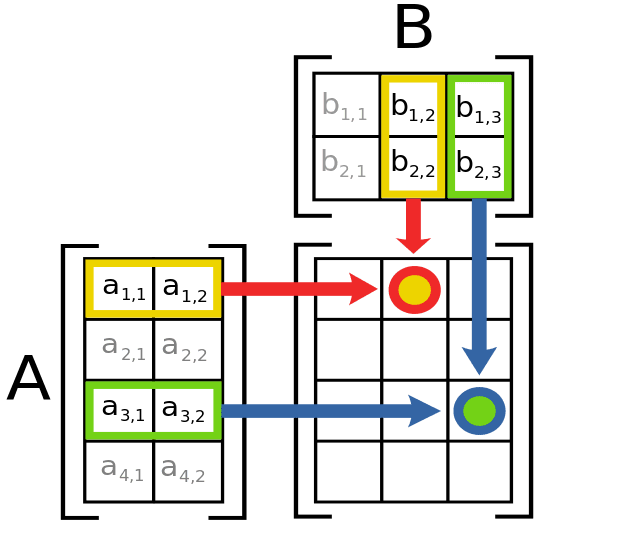
Introduction To Matrices And Matrix Arithmetic For Machine Learning

Dot Product Explained Basic Physics Physics 12th Maths










