Multiplying Rotation Matrices
You might as well look at Tommy s answer. Have a play with this 2D transformation app.

Describing Rotation In 3d Robot Academy
The angle sum formulae for sine and cosine can be derived this way.
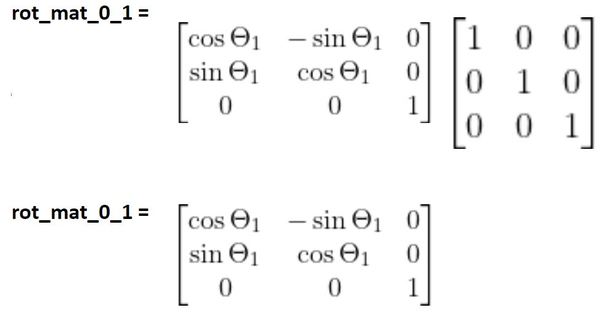
Multiplying rotation matrices. For a column vector we pre-multiply the rotationtransformation matrix which is in a column-major format. Lets say you have a 3x3 matrix that stores an objects current rotation. 0 R 2 1 2sinsin2 cos2 1 0 Because rotations are actually matrices and because function compositionfor matrices is matrix multiplication well often multiply rotation functionssuch asRR to mean that we are composing them.
That is the rotation matrix R A O operates on the vector x y z by. By premultiplying R_bc by R_sb weve changed the representation of the c frame from the b frame to the s frame as we can verify by inspecting the rotation matrices. Once you have your 3 matrix you can express them as quaternions multiply them together then express that result into another rotation matrix.
Do I use the post multiply or pre multiply. 1 R AB R AO R OB 2 R AB R OB R AO. Now I have came across an issue where I see Mat3x3 rotation matrix being multiplied together to form the spinning cube shown above.
Thus we can writeTheorem 14 asRRR. If we want to express the c frame in s coordinates instead of b coordinates we can perform the matrix multiplication R_sc equals R_sb times R_bc. There are two suggestions that come to mind.
Let us imagine that all I know is the rotation matrix R AO between A and O and the rotation matrix R OB between O and B. The rotation matrix defines the rotation about that centering point and the offset matrix defines the final translation after the rotation. Rotations can be represented by orthogonal matrices there is an equivalence with quaternion multiplication as described here.
As we know by multiplying it with a new 3x3 rotation matrix we will get a brand new rotation matrix. A matrix can do geometric transformations. As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the.
So what is the correct way to determine R AB. To rotate the Δ X Y Z 180 counterclockwise about the origin multiply the vertex matrix by the rotation matrix 1 0 0 1. Depending on how you define your xyz points it can be either a column vector or a row vector.
You end up in the same place either way. Usually an axis vector and a rotation angle is enough to get a rotation matrix. This is the normal way we write a matrix multiplication.
Matrices can also transform from 3D to 2D very useful for computer graphics do 3D transformations and much much more. Since from what I read that post multiply is used when the moving coordinate is rotated with the reference of its own coordinate and pre multiply is used when the moving. User2479595 you should be able to initialize a rotation for each of your axis.
Thanks to all of you who s. That is post-multiplying the rotation R A O by the rotation R O B is given by the matrix R O B. For each xy point that makes up the shape we do this matrix multiplication.
Write the ordered pairs as a vertex matrix. We know from thinking about it that when doing rotations of the plane it doesnt matter whether you first rotate by 30 then by 60 or if you rotate by 60 then 30. NewMat3x3 Mat3x3A Mat3x3B.
Different transformations such as translations rotations scaling and shearing are represented mathematically in different ways. Now my intuition is that 1 is correct ie. I know that both T1 and T2 needs to be multiplied by a rotational matrix but I dont know how to multiply the rotational matrix.
One matrix can also represent multiple transformations in sequence when the matrices are multiplied together. 1 0 0 0 0 1 0 1 0 x y z and so really your post-multiplication operation is given by 2 rather than 1. For example to rotate around a given point the transformations would be 1 the centering matrix to bring that point to the origin 2 the rotation about the center and 3 the final offset to return the origin back to its original location.
An nx1 matrix is called a column vector and a 1xn matrix is called a row vector. To rotate twice just multiply two rotation matrices together. When an object undergoes a transformation the transformation can be represented as a matrix.
1 per month helps. Rotated 90 from where you started. About the method The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one.
Therefore the coordinates of the vertices of Δ X Y Z are X 1 2 Y 3 5 and Z 3 4. If we rotate the coordinate axes we can compute a vector in the new primed coordinates from the original vector by multiplying by a Rotation Matrix. You da real mvps.
First rotation about z axis assume a rotation of a in an anticlockwise direction this can be represented by a vector in the positive z direction out of the page. Thanks to all of you who support me on Patreon.

Robotics Position And Orientation
Rotation Matrix Derivation The 3 D Global Spatial Data Model

Concatenating Translation And Rotation Matrix What Am I Doing Wrong Mathematics Stack Exchange
How To Find The Rotation Matrices For Robotic Arms Automatic Addison
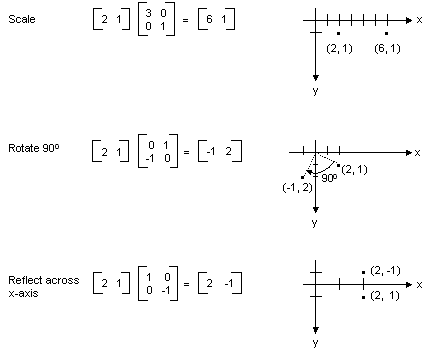
Matrix Representation Of Transformations Win32 Apps Microsoft Docs
Transforming Objects Handle Graphics Objects Graphics
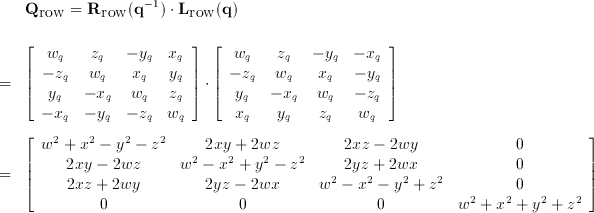
Cs184 Using Quaternions To Represent Rotation

How To Rotate An Object Around One Of Its Local Axis In Directx11 Stack Overflow

Multiplication Order Of Rotation Matrices Mathematics Stack Exchange

Matrix Multiplication 2 000 Things You Should Know About Wpf
Rotation Matrix Wikipedia Republished Wiki 2

Using Pre Multiply Or Post Multipy For Rotational Matrix To Get A New Homogenous Transformation Matrix Robotics Stack Exchange

Describing Rotation In 3d Robot Academy

Understanding The Math Behind Rotating Around An Arbitrary Axis In Webgl Stack Overflow

Applicaton Of Matrix Multiplication Transformations Youtube

