Orthogonal Matrices And Inner Product

29 Apr, 2021

Aunitary operatorT on an inner product spaceVis an invertible linear map satis-fying TTITT. Hu vwi huwi hvwiand h uvi huvi iii Conjugate symmetry.

Part 23 Orthonormal Vectors Orthogonal Matrices And Hadamard Matrix By Avnish Linear Algebra Medium

Both Omnand QSare smooth manifolds 11and can both be thought of as submanifolds of Rmnwith inner productABtrABTVecATVecB.

Orthogonal matrices and inner product. Two vectors uv 2Rn are orthogonal if uv 0. The length of a vector is the square root of the dot product of a vector with itself. Commuting with inner product and then specializing using basis.

The orthogonal matrix has all real elements in it. If U is a subset of an inner-product space V then the orthogonal complement of U is defined as Ubotvin V. Let n 2 and let W be the subspace of M n R consisting of all matrices whose trace is zero.

Is defined as follows. Matrix-vectorproduct ifA 2Rmn hasorthonormalcolumnsthenthelinearfunction fx Ax preservesinnerproducts. A vector space endowed with an inner product is called an inner.

This identification follows from VecRmnRmn. Orthogonal Decomposition If U is a subspace of an inner-product. MacBook Pro Moving to another question will save this response.

V b1b2bnT 2 Rn. The norm of the vector is a vector of unit length that points in the same direction as. Two vectors are orthogonal if and only if kuvk2 kuk2kvk2.

I hope this is a satisfactory answer. The product of two orthogonal matrices is also an orthogonal matrix. V V F satisfying i hvvi 0 with equality if and only if v 0 iiLinearity in the rst slot.

This well-known theorem has numerous different proofs. However I prefer doing the general case first ie. The collection of the orthogonal matrix of order n x n in a group is called an orthogonal group and is denoted by O.

Are orthogonal if and only if In the inner product space of 2-square matrices with the inner product truv the two matrices - O 0-1. This isnt necessary sinceunitaryencompasses both real and complex spaces. Inner products allow the rigorous introduction of intuitive geometrical notions.

This does using the above identification become equivalent to the definition you know. Two vectors are orthogonal if and only if kuvk2 kuk2kvk2. Otis any real number Moving to another question will save this response.

If A a i j and B b i j for 1 ij n are elements in M n R define their inner-product by A B i j 0 n a i j b i j Identify the subspace W of elements orthogonal to the subspace W. Let V be an inner product space with inner product. A list of nonzero vectors e1emofV is called orthogonal if eiej 0 forall1 i j m.

The notion of inner product allows us to introduce the notion of orthogonality together with a rich family of properties in linear algebra. If Vis real we usually call theseorthogonal operatorsmatrices. AxTAy xTATAy xTy preservesnorms.

The transpose of the orthogonal matrix is also orthogonal. In mathematics an inner product space or a Hausdorff pre-Hilbert space is a vector space with a binary operation called an inner product. Otis any real number.

INNER PRODUCT ORTHOGONALITY. Two vectors uv 2Rn are orthogonal if uv 0. Left langle v u right rangle 0 text for all uin U Theorem.

The inner product hi satisﬂes the following properties. As we will see later orthonormal bases have very special properties that simplify many calculations. This well-known theorem has numerous different proofs.

Notice that there exists a matrix QOmnwith sign pattern Sif and only if the intersection of Omnand QSis nonempty. Inner Product Spaces and Orthogonality week 13-14 Fall 2006 1 Dot product of Rn The inner product or dot product of Rn is a function hi deﬂned by huvi a1b1 a2b2 anbn for u a1a2anT. The notion of inner product allows us to introduce the notion of orthogonality together with a rich family of properties in linear algebra.

However in general you can define an orthogonal matrix as commuting with the inner product. Aunitary matrixis a matrix satisfyingAAI. The Inner or Dot Product of the vectors.

This operation associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors often denoted using angle brackets as in. Huvi hvui for all uvw2V and all 2F. All identity matrices are orthogonal matrices.

Moving to another question will save this response estion 8 and In the inner product space of 2-square matrices with the inner product truy the two matrices are orthogonal and only 1. 3 Inner products An inner product on a vector space V over F is a function hi. We now deﬁne the notion of orthogonal and orthonormal bases of an inner product space.

The distance between two vectors is the length of their difference. Note that an orthogonal matrix satisﬁesATAI.

For Any Inner Product Can We Always Find A Symmetric Orthonormal Basis Mathematics Stack Exchange

Beyond Vectors Hungyi Lee Introduction Many Things Can

Inner Dot Product Of Two Vectors Applications In Machine Learning

Inner Product Space

6 2 Angle And Orthogonality In Inner Product Spaces Youtube

Linear Algebra Inner Product Space Gram Schmidt Orthogonal Complement Mat223 Past Test Youtube

Chapter 7 Inner Product Spaces Ppt Download

Lecture 11 Inner Product Space Ppt Download

For Any Inner Product Can We Always Find A Symmetric Orthonormal Basis Mathematics Stack Exchange

How Can An Inner Product Be Defined Through A Proof Mathematics Stack Exchange

For Any Inner Product Can We Always Find A Symmetric Orthonormal Basis Mathematics Stack Exchange

Part 23 Orthonormal Vectors Orthogonal Matrices And Hadamard Matrix By Avnish Linear Algebra Medium

If The Inner Product Of Two Matrices Is Zero What Does That Mean

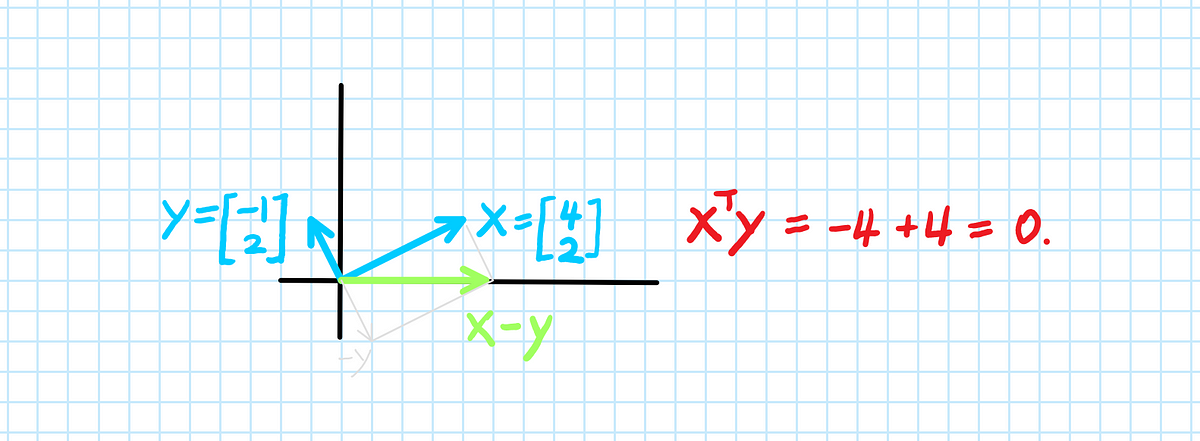
Why Is The Dot Product Of Orthogonal Vectors Zero By Aerin Kim Towards Data Science

Why Does The Fact That Tv Is Orthogonal To V For All V Implies T Is The Zero Operator Break Down For Real Inner Product Spaces Mathematics Stack Exchange

Linear Algebra Inner Product Space Orthogonality Flashcards Quizlet

Dot Product Vs Inner Product Mathematics Stack Exchange