Dot Product With Orthogonal Matrix
The inverse of an orthogonal matrix Ais AT. In particular in a QR-decomposition of an n n-matrix the Qis orthogonal.

Cross Product Introduction Formula Vectors Video Khan Academy
In fact every orthogonal matrix C looks like this.

Dot product with orthogonal matrix. Orthogonal matrices preserve angles and length. Or we can say if the dot product of two vectors is zero then they are orthogonal. The product of two orthogonal matrices is orthogonal.
The columns of any orthogonal matrix form an orthonormal basis of Rn. Their dot product is 0. Grinfelds Tensor Calculus textbookhttpslemmaprep - C.
In this section we show how the dot product can be used to define orthogonality ie when two vectors are perpendicular to each other. Also I would like to show that Orthogonal matrices preserve dot product and I found that. An n n-matrix is orthogonal if AT A id n.
HttpsbitlyPavelPatreonhttpslemmaLA - Linear Algebra on LemmahttpbitlyITCYTNew - Dr. The dot product of the two column matrices that represent them is zero. Subsection 612 Orthogonal Vectors.
Orthonormal Vectors If vector x and vector y are also unit vectors then they are orthonormal. The dot product of two orthogonal vectors is zero. Note as well that often we will use the term orthogonal in place of perpendicular.
Since 0 x 0 for any vector x the zero vector is orthogonal to every vector in R n. This works because the ij entry of ATA is the dot product of v_i and v_j. Another notation that is used for the inner product is hxyi.
From this it follows that orthogonal matrices preserve the. I found that it is related with the determinant. An orthogonal matrix is an invertible matrix Csuch that C 1 CT.
Third of three videos on dot products. Now if two vectors are orthogonal then we know that the angle between them is 90 degrees. We discuss orthogonal matrices and finally prove that v dot w equals v w costheta.
If then is orthogonal to every row in A because the dot product between each row in A and the vector is zero. Compute ATA the product of the transpose of A with A. Dot Product of Orthogonal Matrix When we learn in Linear Algebra if two vectors are orthogonal then the dot product of the two will be equal to zero.
Dot Products Transposes and Orthogonal Projections David Jekel November 13 2015 Properties of Dot Products Recall that the dot product or standard inner product on Rn is given by xy x 1y 1 x ny n. Then the matrix C 2 4v 1 v n 3 5 is an orthogonal matrix. Since the rows of A span row space is orthogonal to.
Recall also that the dot product of two vectors and can be written as. Recall that an real matrix is called orthogonal if where denotes the transpose. However I do not know how to show it.
If two vectors are orthogonal then their dot product is zero whereas their cross product is maximum. Let fv 1v ngbe an orthonormal basis for Rn. Also if the magnitude of the two vectors is equal to one then they are called orthonormal.
It says that the determinant of an orthogonal matrix is pm1 and orthogonal transformations and isometries preserve volumes. The result is the identity if and only if v_1 v_k are orthonormal. X y means x y 0.
Two vector x and y are orthogonal if they are perpendicular to each other ie. Two vectors x y in R n are orthogonal or perpendicular if x y 0. This is equivalent to the columns of Abeing an orthonormal basis of Rn.
The result of the dot product of two vectors is a scalar quantity whereas the result of the cross product of two vectors is a vector quantity. Only the relative orientation matters. The result is diagonal if and only if v_1 v_k are orthogonal.
Since if then is orthogonal to every column in A. The dot product gives us a very nice method for determining if two vectors are perpendicular and it will give another method for determining when two vectors are parallel.
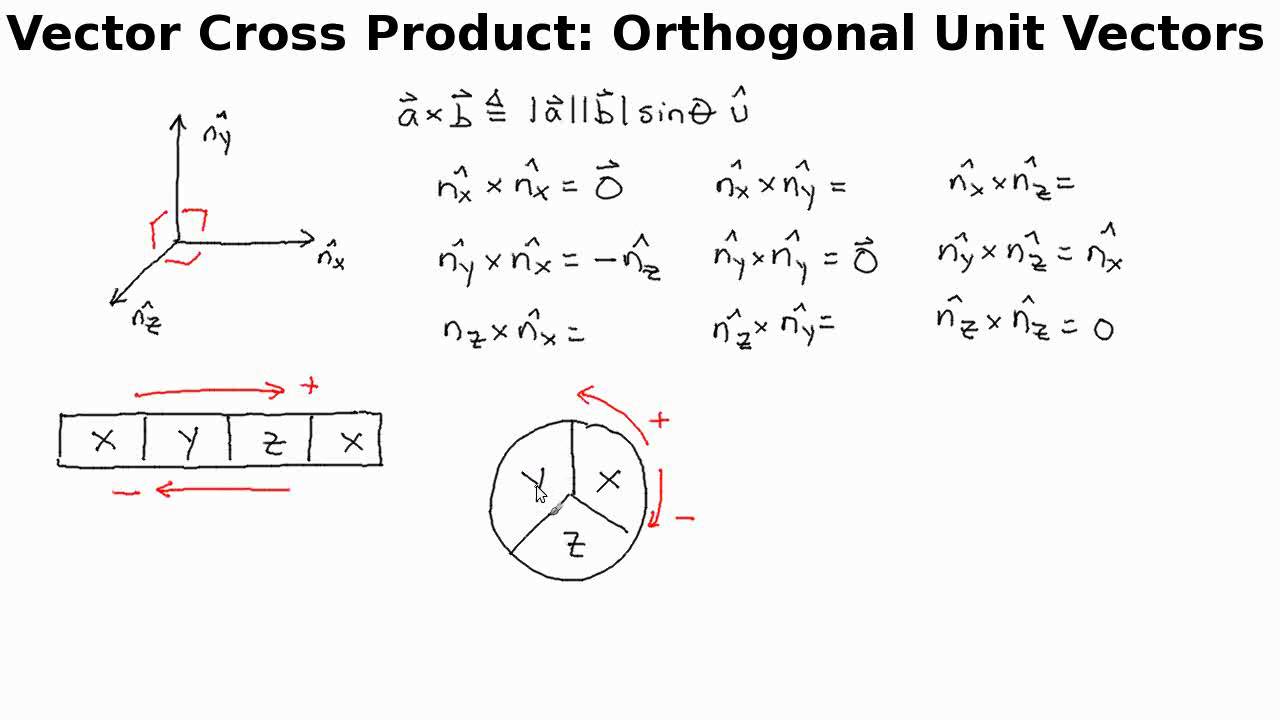
Vector Cross Product Orthogonal Unit Vectors Youtube
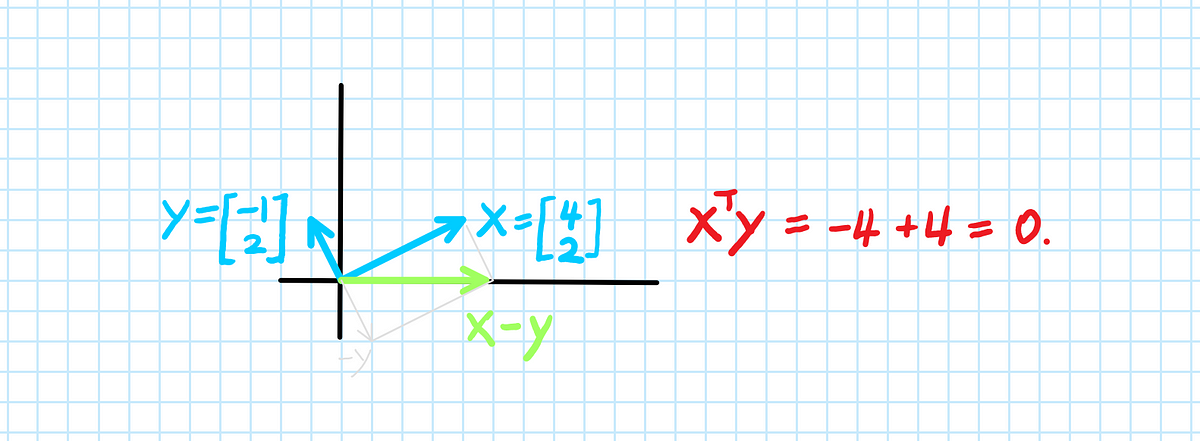
Why Is The Dot Product Of Orthogonal Vectors Zero By Aerin Kim Towards Data Science

Linear Algebra 9 Properties Of Orthogonal Matrices By Jun Jun Devpblog Medium

Matrices As Tensor Network Diagrams Matrix Matrix Multiplication Networking
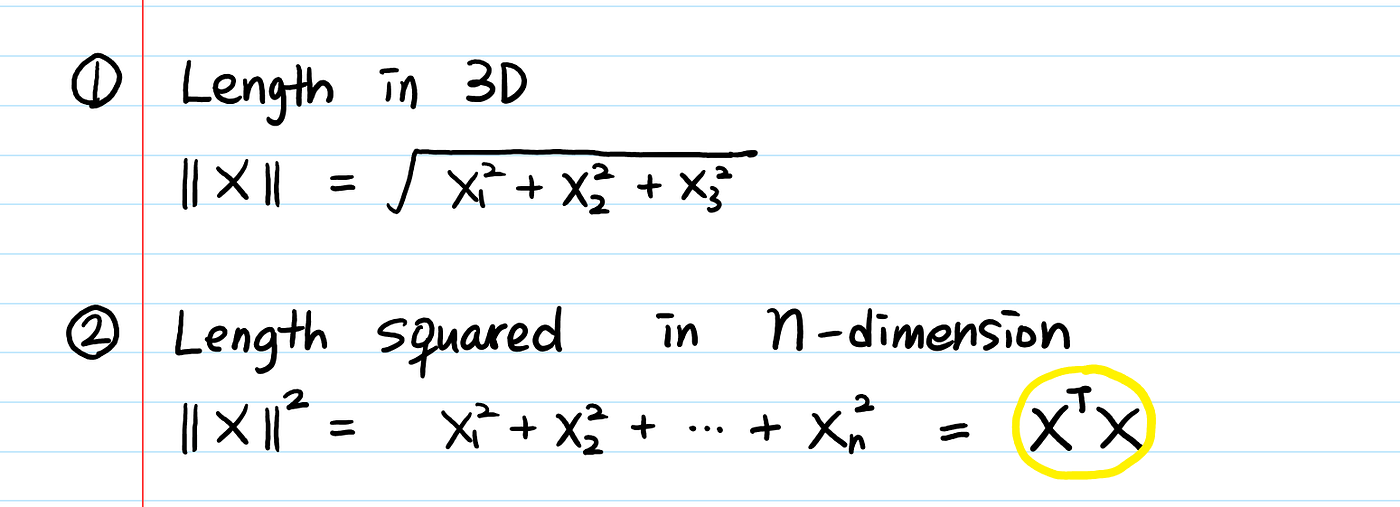
Why Is The Dot Product Of Orthogonal Vectors Zero By Aerin Kim Towards Data Science

Part 23 Orthonormal Vectors Orthogonal Matrices And Hadamard Matrix By Avnish Linear Algebra Medium

Orthogonal And Orthonormal Vectors In Linear Algebra Geeksforgeeks

Why Is The Dot Product Of Orthogonal Vectors Zero By Aerin Kim Towards Data Science

Linear Algebra Lecture 37 Inner Product Length And Orthogonality Youtube

Calculus 3 The Dot Product Youtube

How To Identify An Orthogonal Orthonormal Matrix Mathematics Stack Exchange
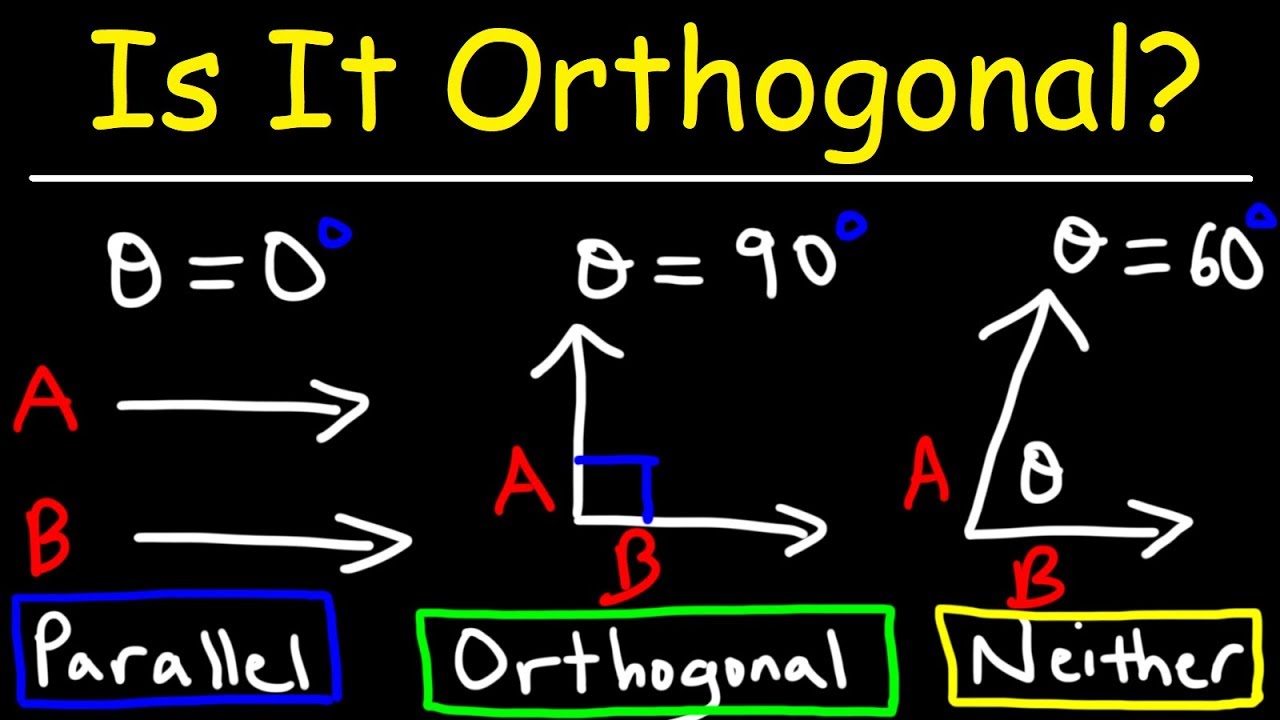
Are The Two Vectors Parallel Orthogonal Or Neither Youtube

Part 23 Orthonormal Vectors Orthogonal Matrices And Hadamard Matrix By Avnish Linear Algebra Medium
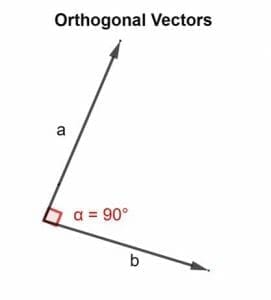
Orthogonal Vector Explanation And Examples




