Invertible Symmetric Matrix Orthogonal
Semidefinite means that the matrix can have zero eigenvalues which if it does makes it not invertible. 12 Hat Matrix as Orthogonal Projection The matrix of a projection which is also symmetric is an orthogonal projection.

15 Inverse Of A Square Matrix Dear Students Mathematics Lecture
An orthogonal matrix is a square invertible matrix U U such that U 1 U T U 1 U T.
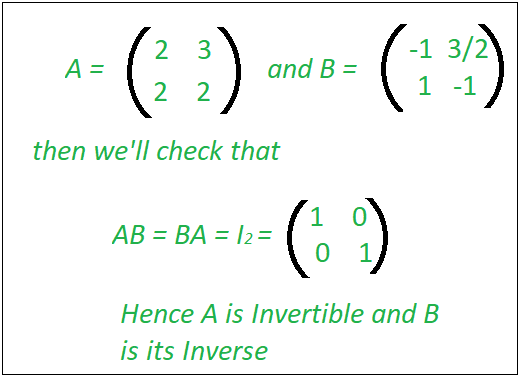
Invertible symmetric matrix orthogonal. Because the matrix A is singular there are in nite number of solutions. Which shows that P is orthogonal proving the claim. The determinant of the orthogonal matrix has a value of 1.
To prove this we need the following useful fact about symmetric matrices. A matrix can be both orthogonal and not have an inverse. Diagonal entry inverse matrix inverse matrix of a 2 by 2 matrix linear algebra symmetric matrix Next story Find an Orthonormal Basis of R3 Containing a Given Vector Previous story If Every Proper Ideal of a Commutative Ring is a Prime Ideal then It is a Field.
An n nmatrix A is orthogonal if i its inverse A 1 exists and ii AT A 1. See 8 9 13 for discussions. It is clearly symmetric but cannot be orthogonal as it doesnt have an inverse because it has a 0.
De nition 1 Let U be a d dmatrix. These two conditions can be re-stated as follows. Theorem 823 If A is annn symmetric matrix then AxyxAy for all columnsxandyinRn3 Proof.
Let ij denote the Kronecker symbol. Because AT A we get AxyAxTyxTATyxTAyxAy Theorem 824. Let Abe any d dsymmetric matrix.
A positive semidefinite matrix is symmetric so it has an orthogonal set of eigenvectors and so where is an orthogonal matrix and is diagonal with non-negative entries. In particular they are not equal to one hence A I is invertible. A matrix can be both symmetric and skew-symmetric.
In the same way the inverse of the orthogonal matrix which is A-1 is also an orthogonal matrix. The matrix is symmetric implies that they are orthogonal. Adoes not allowLUas we need to permute its rows to make itLU-factorable but by the Spectral Theorem it allowsQQ1and thenSS1.
The matrix B is orthogonal means that its transpose is its inverse. However A2I 6AsoAis notprojection. Since A I 1 A I v λ 1 λ 1 v and λ 1 λ 1 1 we have the desired result.
It is orthogonal because AT A 1 cos sin sin cos. Consider a 22 matrix with all its entries as 1. A matrix must be either symmetric or skew symmetric.
In other words Pei vi for each i. Answered Jan 9 15 at 844. Ij 0 if i 6 j and ii 1.
A matrix must be either orthogonal or not have an inverse. It is symmetric in nature. There exists an orthogonal matrix.
The eigenvalues of the orthogonal matrix also have a value of 1 and its eigenvectors would also be orthogonal and real. Special types of square matrix Diagonal matrices lower and upper traingular matrices symmetric and antisymmetric matrices orthogonal matri-ces AT A 1 Hermetian matrix A Ayor Ay A unitary matrix Ay A 1 essentially a generalization of. So an orthogonal matrix is necessarily invertible whereas that is not necessary for a symmetric matrix.
1A square matrix A is a projection if it is idempotent 2A projection A is orthogonal if it is also symmetric. Ais permutation so it is also invertible orthogonal and MarkovIt is symmetric so it is also diagonalizable. Consider A cos sin sin cos.
We can show that both H and I H are orthogonal projections. C i C j δ i j. Because U U is invertible and U T U 1 U T U 1 and U U T I U U T I.
O T O C i C j 1 i j n I n. Ill-posed problems with a symmetric matrix A determine iterates in the range of the matrix to ensure that the iterates are orthogonal to the null space of the matrix. Such a matrix is necessarily square.
A matrix B is symmetric means that its transposed matrix is itself. Where is a free parameter. This implies that UUT I by uniqueness of inverses.
These methods allow the matrix A to be nonsymmetric and even nonsquare but they are not able to exploit symmetry in a significant manner when A is symmetric and possibly indefinite. We have the vis are orthonormal vi vj ij 8ij et iP tPe j ij 8ij PtP I. To show that A I 1 A I is orthogonal it is sufficient to show that A I 1 A I v 1 for all unit eigenvectors v.
A symmetric matrix is a matrix A A such that A AT A A T. Next we claim that PtAP is diagonal. For instance the Minimal Residual MR method by Paige and Saunders 20 is a popular iterative method for the solution of linear systems.
P be the matrix whose columns are v1vn. O T C 1 C n T C 1 T C n T so we get. If the matrix is orthogonal then its transpose and inverse are equal.
The matrix U is called an orthogonal matrix if UTU I. Most important and useful property of symmetric matrices is that their eigenvalues behave very nicely. Recall that xyxTy for all columns x and y.
The answer is NO. 2 4 23 13 23 23 23 13 13 23 23 3 5 An orthogonal matrix must be formed by an orthonormal set of vectors. Fact 2 Spectral Theorem.
The following is a 3 3 orthogonal matrix. Let C i the i th column of the orthogonal matrix O then we have. It is the purpose of the present paper to describe numerical methods that are tailored for the solution of large linear discrete ill-posed problems with a.

Orthogonal Matrix An Overview Sciencedirect Topics

Introduction To Diagonal And Symmetric Matrices Unit And Orthogonal Vectors Using Python Numpy Examples And Drawings

Question1 A I Suppose A And B Are Nonsingular Chegg Com

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange
Orthogonal Matrices Linear Algebra

Linear Algebra 9 Properties Of Orthogonal Matrices By Jun Jun Devpblog Medium

Orthogonal Matrices Symmetric Matrices Hungyi Lee Outline Orthogonal

Chapter 7 Symmetric Matrices And Quadratic Forms Flashcards Quizlet

Linear Transformation Standard Matrix The Standard Basis Logic Math Mathematics Math

Question Video Finding Unknown Elements Of A Symmetric Matrix Nagwa

Symmetric Skew Symmetric And Orthogonal Matrix Linear Algebra L2 P1 Youtube

Orthogonal Matrices Based On Excelent Video Lectures By

What Are The General Form Of Eigenvalues Of An Orthogonal Matrix Mathematics Stack Exchange

If A Is A Symmetric Matrix And B Is A Skew Symmetric Matrix Youtube
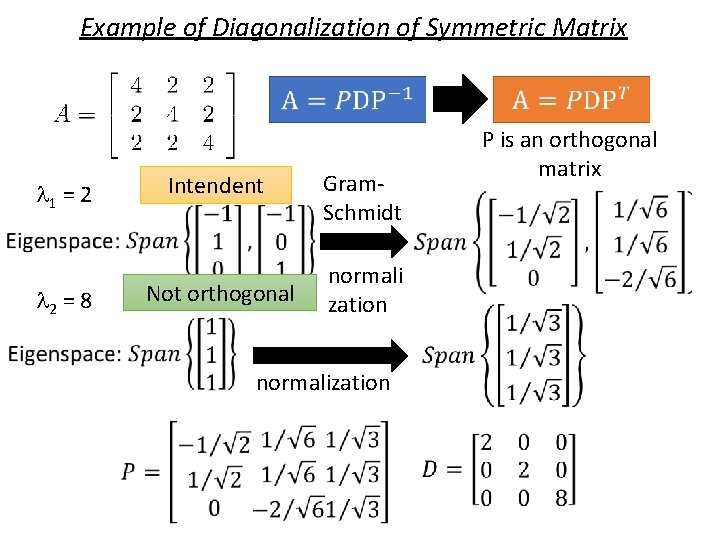
Orthogonal Matrices Symmetric Matrices Hungyi Lee Outline Orthogonal

Check If A Matrix Is Invertible Geeksforgeeks

Proof For Why Symmetric Matrices Are Only Orthogonally Diagonalizable Mathematics Stack Exchange

A Which Of The Matrices Are Orthogonal Has Chegg Com

