Matrix Multiplication Using Divide And Conquer Code In C
Void get_matrix_b. Matrix Multiplication in C without using.

Divide And Conquer Divide And Conquer Algorithms Consist
We then use these results to compute Cs submatricies.

Matrix multiplication using divide and conquer code in c. Solving the procedure manually would require nine separate calculations to obtain each element of the final matrix X. The c cAisBsj assignment statement will be executed exactly n m k times. A Divide-And-Conquer Algorithm for Matrix Multiplication Note.
Fori0i. Printf Enter the 4 elements of first matrix. Float matrix_a 3 3.
Indent consistently with 4 spaces insert spaces around binary operators after and. A e b g a f b h c e d g c f d h. It has less time complexity.
Following is simple Divide and Conquer method to multiply two square matrices. I reformatted your code so I could analyze it. C code of two 2 by 2 matrix multiplication using Strassen algorithm.
Gcc -o exec c. There seems to be missing code in the matrixMultiply function. There are some procedures.
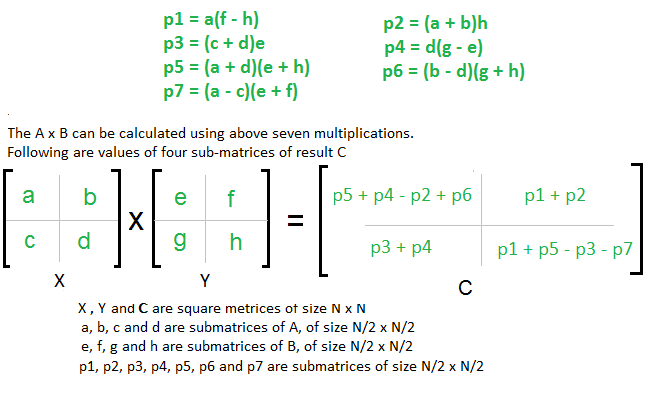
For two 22 matrices a and b where A. Matrix A a b matrix B e f c d g h There will be 8 recursive calls. Calculate following values recursively.
Int main. Ae bg af bh ce dg and cf dh. Ae bg af bh ce dg and cf dh.
Float matrix_b 3 3. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. Include include include class Matrix private.
A C Program to Multiply two Matrices. Divide And Conquer Algorithm. Float matrix_c 3 3.
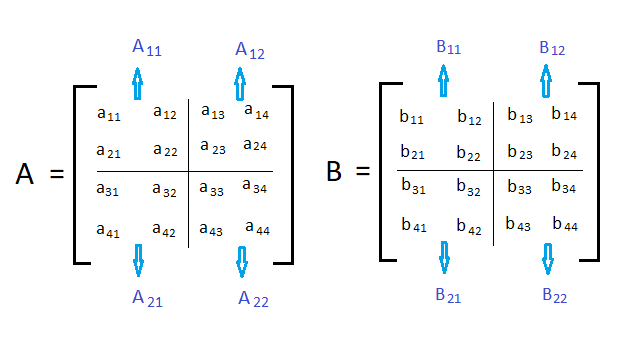
Int a 2 2b 2 2c 2 2ij. For your android. Consider two matrices A and B with 4x4 dimension each as shown below The matrix multiplication of the above two matrices A and B is Matrix C where c11 a11 b11 a12 b21 a13 b31 a14 b41 1 c 11 a 11 b.
This strategy is called Divide and Conquer. Divide and Conquer Method. Consider the following matrices A and B.
For the sake of simplicity but without loss of generality assume that we are multiplying to square nn matrices A and B ie m n and k n. Divide and conquer matrix multiplication example. Procedure of Strassen matrix multiplication.
Count of an element in a matrix using Divide Conquer. My idea is to divide the matrix in 4 sub-matrices till all coordinates are equal it means that there is an element could be my number or not. Following is simple Divide and Conquer method to multiply two square matrices.
Divide the matrix then use the Strassens formulae. C is the resultant matrix of A and B. Here the implementation of Strassens algorithm for matrix multiplication is kind of incorrect here.
Divide a matrix of order of 22 recursively till we get the matrix of 22. Use the previous set of formulas to carry out 22 matrix multiplication. Below is Recursive Matrix Multiplication code.
K is used to know current column number of A. Void multiply_matrices. You allocate the resulting matrix C but you use it as an input to initialize the intermediary matrices c11 c21 c21 and c22.
Now Lets try similar implementation using Threads in c. Strassens Matrix Multiplication Algorithm uses divide and conquer strategy. Divide And Conquer Algorithm Code.
Void get_matrix_a. Gcc -o exec c. MatrixMultiplya b n arows let c be a new n x n matrix if n 1 c11 a11 b11 else partition a b and c C11 MatrixMultiplyA11 B11 MatrixMultiplyA12 B21 C12 MatrixMultiplyA11 B12 MatrixMultiplyA12 B22 C21 MatrixMultiplyA21 B11 MatrixMultiplyA22 B21 C22 MatrixMultiplyA21 B12 MatrixMultiplyA22 B22 return c.
The matrix multiplication takes place as shown below and this same procedure is is used for multiplication of matrices using C. 2 Calculate following values recursively. Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram.
It is of order On3Watch this video for the correct i. I need to count how many times a number finds in the matrix using DC. With the assumptions about we obtain our bound on the runtime of the algorithm.
In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. Separators and between keywords and this improves readability a lot. Lets implement it using C programming.
It can be observed that we can contain four n2n2 submatrices from A B and their product C. CC Recursive code for Matrix Multiplication include const int MAX 100. A C Program to Multiply two Matrices.
This was a small try in implementing Java threads explained byt taking the example of matrix multiplication using 3 different algorithms. Void multiplyMatrixRecint row1 int col1 int AMAX int row2 int col2 int BMAX int CMAX Note that below variables are static i and j are used to know current cell of result matrix C. 1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram.
These nine separate calculations have been done using very few lines of code involving loops and function in this C program for Matrix Multiplication.

Matrix Multiplication Using Divide And Conquer Time Complexity Stack Overflow

Strassen Matrix Multiplication Method Using Divide And Conquer Youtube
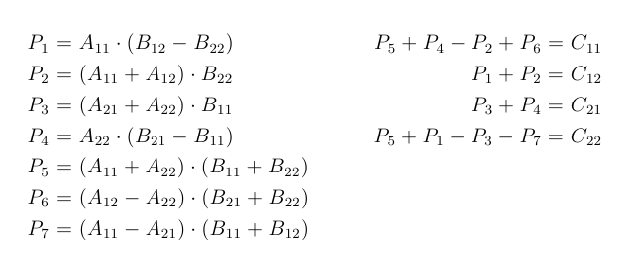
Strassen Matrix Multiplication C The Startup

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Divide And Conquer Matrix Multiplication Programmer Sought

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

Java Math Decrementexact Explanation With Example Code Vs Color Python Programming Python Java Programming Tutorials
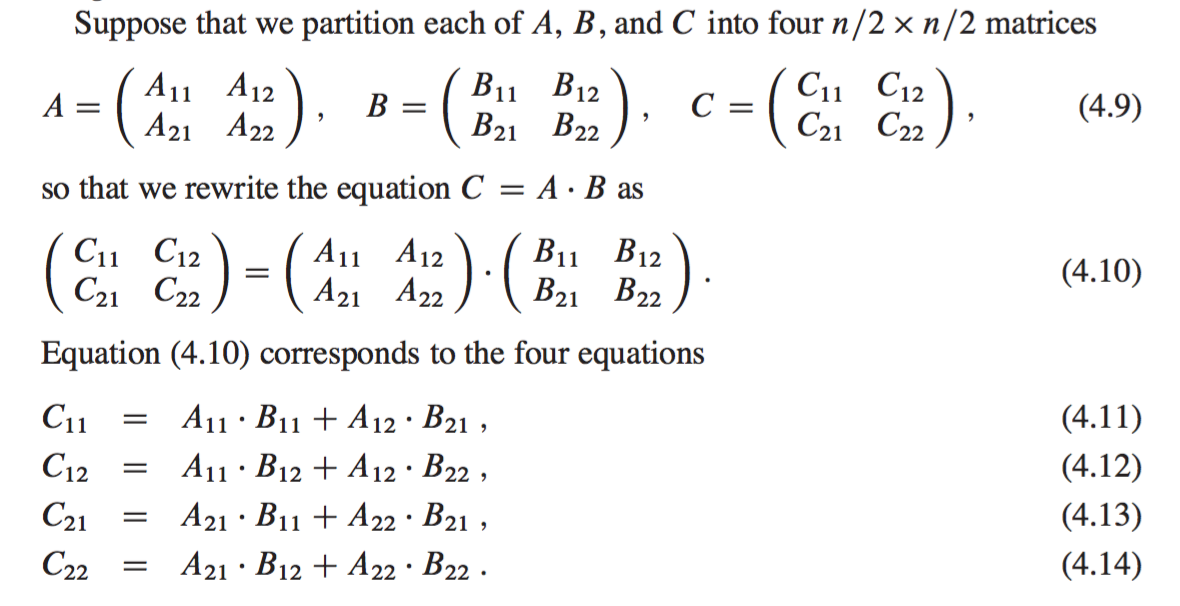
Matrix Multiplication Using The Divide And Conquer Paradigm

Matrix Multiplication Using Divide And Conquer Time Complexity Stack Overflow
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

Divide And Conquer Matrix Multiplication Programmer Sought
Strassen S Matrix Multiplication Algorithm Know Program

Karatsuba Algorithm For Fast Multiplication Using Divide And Conquer Algorithm Geeksforgeeks
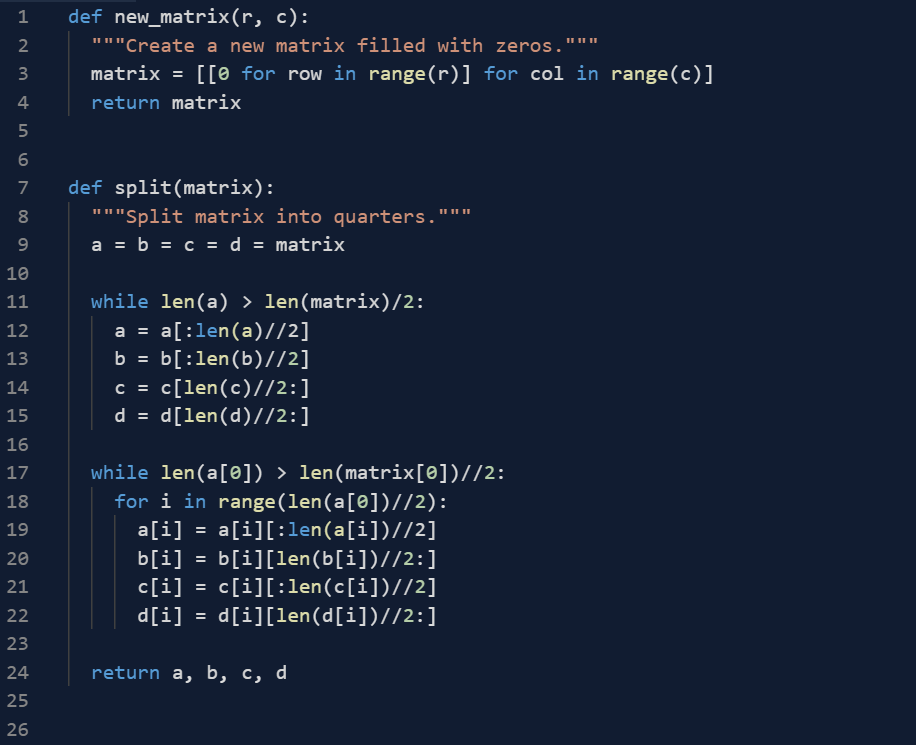
Solved Implement Strassen S Divide Conquer Matrix Multiplication Algorithm Python Multiplying Two Q42436813

Divide And Conquer Set 5 Strassen S Matrix Multiplication Tutorialspoint Dev
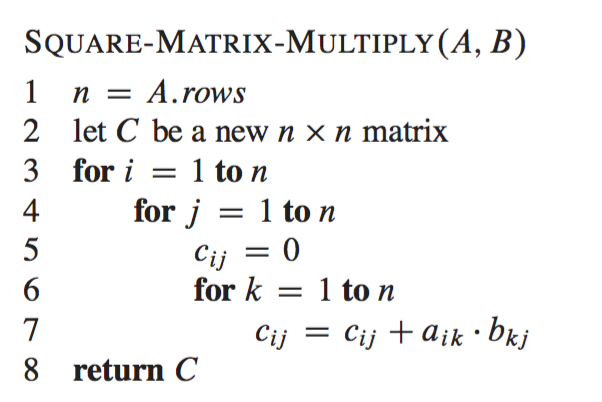
Matrix Multiplication Using The Divide And Conquer Paradigm

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Pin On Mercedes Benz Wallpaper
