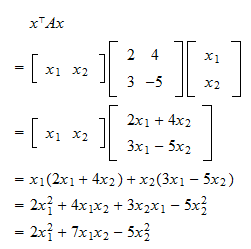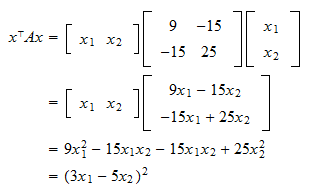Matrix Symmetric Positive Definite
Our final definition of positive definite is that a matrix A is positive definite if and only if it can be written as A RTR where R is a ma trix possibly rectangular with independent columns. Semidefinite matrix is a Hermitian matrix A2M n satisfying hAxxi0 resp.

The Symmetric Positive Definite Matrix A Product Of Chegg Com
Positive definiteness PD or semidefiniteness PSD requires the eigen values of the matrix either to be 0 or 0 respectively.

Matrix symmetric positive definite. If A 0 then as xTx 0 we must have XTAX 0. The definition seems to make sense for general square matrices. 2 1 0 1 2 1 0 1 2 3 -L- L1 70 7 jcsive If x is an eigenvector of A then x 0 and Ax Ax.
The covariance between two variables is defied as σ x y E x E x y E y. Monte-Carlo methods are ideal for option pricing where the payoff is dependent on a basket of underlying assets For a basket of n assets the correlation matrix Σ is symmetric and positive definite therefore it can be factorized as Σ LLT where L is a lower triangular matrix. LetAbe a real symmetric matrix.
Remember that the term positive definiteness is valid only for symmetric matrices. Why must M be symmetric. This way you dont need any tolerancesany function that wants a positive-definite will run Cholesky on it so its the absolute best way to determine positive-definiteness.
Note that using our energy-baseddefinition its easy to prove that if A RTR then A is positive definite. I have listed down a few simple methods to test the positive definiteness of a matrix. Satisfies all the inequalities but for.
This had an effect on the output of qr which in turn had an effect on the output of chol which is what mvncdf used to test whether the matrix is positive definite. Matrix is symmetric positive definite. A positive definite resp.
Before giving verifiable characterizations of positive definiteness resp. Hence the matrix has to be symmetric. Methods to test Positive Definiteness.
0 for all x2Cn nf0g. In order to perform Cholesky Decomposition of a matrix the matrix has to be a positive definite matrix. 2Thereason for this is that the eigenvectors of a symmetric n x n matrix span all of.
We write A0 respA 0 to designate a positive definite resp. The entries in the diagonal matrix are the square roots of the eigenvalues. The problem of estimating the noise covariance matrices in estimation algorithms is considered first.
Matrices that were near the boundary of being positive definite might now be calculated as being non positive-definite. Example-Is the following matrix positive definite. For OS-X the change was between R2015b and R2016a.
A λI 2 λ 8λ 11 0 ie. If every eigenvalue ofAis positive thenAis positive definite. Matrices quadratic-forms positive-definite symmetric-matrices.
Ans 33 10000 -10000 0 0 20000 0 0 0 26458. The determinant of a positive definite matrix is always positive but the de. Singular Value Decomposition A DUVT gives perfect bases for the 4 subspaces Those are orthogonal matrices U and V in the SVD.
Satisfying these inequalities is not sufficient for positive definiteness. If A and B are both symmetric or Hermitian and B is also a positive-definite matrix the eigenvalues λ i are real and eigenvectors v 1 and v 2 with distinct eigenvalues are B-orthogonal v 1 Bv 2 0. For example the matrix.
Their columns are orthonormal eigenvectors of AAT and ATA. By making particular choices of in this definition we can derive the inequalities. This equation doesnt change if you switch the positions of x and y.
A necessary condition in any quadratic programming to be convex is the matrix Q in the formulation x Q x to be positive definite or positive semidefinite. The drawback of this method is that it cannot be extended to also check whether the matrix is symmetric positive semi-definite where the eigenvalues can be positive or zero. Determinants of a symmetric matrix are positive the matrix is positive definite.
In this case xTAx AxTx. A particularly important class of systems are the linear gradient flows in which AT is a symmetric positive definite matrix. A real matrix is symmetric positive definite if it is symmetric is equal to its transpose and.
According to Theorem 823 all the eigenvalues of K are real and positive and so the eigenvalues of the negative definite. A symmetric matrix M is positive definite if x T M x 0 for all vectors x 0. A correct covariance matrix is always symmetric and positive semi definite.
In this case eigenvectors can be chosen so that the matrix P defined above satisfies. Adaptive estimation and identification algorithms involving unknown symmetric and positive definite SPD matrix-valued parameters are ubiquitous in engineering applications. Its eigenvalues are the solutions to.
Positive definite symmetric matrices both ATA and ATCA are positive definite 2. An adaptive Kalman filter to estimate the noise covariance matrix of. The matrix is symmetric and its pivots and therefore eigenvalues are positive so A is a positive definite matrix.
In addition to just finding the nearest positive-definite matrix the above library includes isPD which uses the Cholesky decomposition to determine whether a matrix is positive-definite. It is positive semidefinite if and only if its eigenvalues are nonnegative. Theorem C6 The real symmetric matrix V is positive definite if and only if its eigenvalues are positive.

Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Let A Be A 3 X 3 Symmetric Positive Definite Matrix Chegg Com

Let A Be A Symmetric Positive Definite Matrix Show Chegg Com
What Is A Positive Definite Matrix By Aerin Kim Towards Data Science

Positive Definite Sequence And Its Corresponding Determinant Mathematics Stack Exchange

Example Symmetric Positive Definite Matrix And Its Cholesky Factor Download Scientific Diagram
How To Check If A Matrix Is Positive Definite Quora
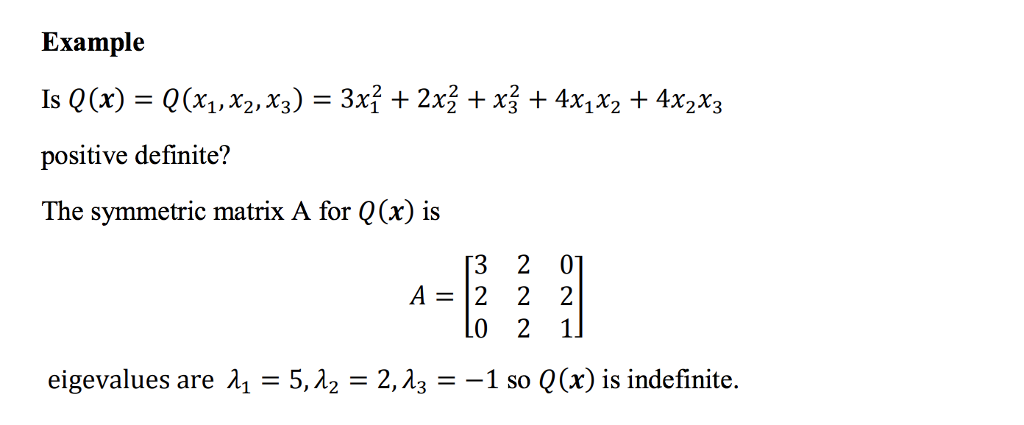
Example 7 3 Page 533 Let A Be A Symmetric Positive Chegg Com
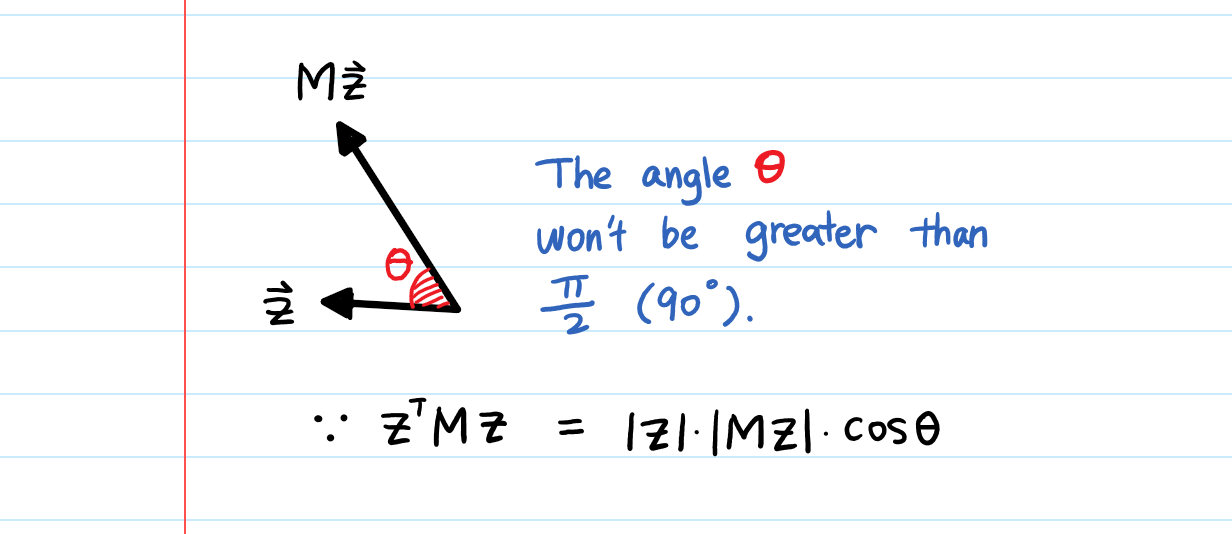
What Is A Positive Definite Matrix By Aerin Kim Towards Data Science

How To Prove That A Matrix Is Positive Definite Youtube

What Does A Positive Definite Matrix Have To Do With Cauchy Schwarz Inequality Mathematics Stack Exchange

For A Symmetric Positive Definite Matrix Why Does Each Diagonal Element Exceeds The Small Eigenvalue Mathematics Stack Exchange

Note Set 23a Totally For Sure Positive Definite Matrices Matrixology
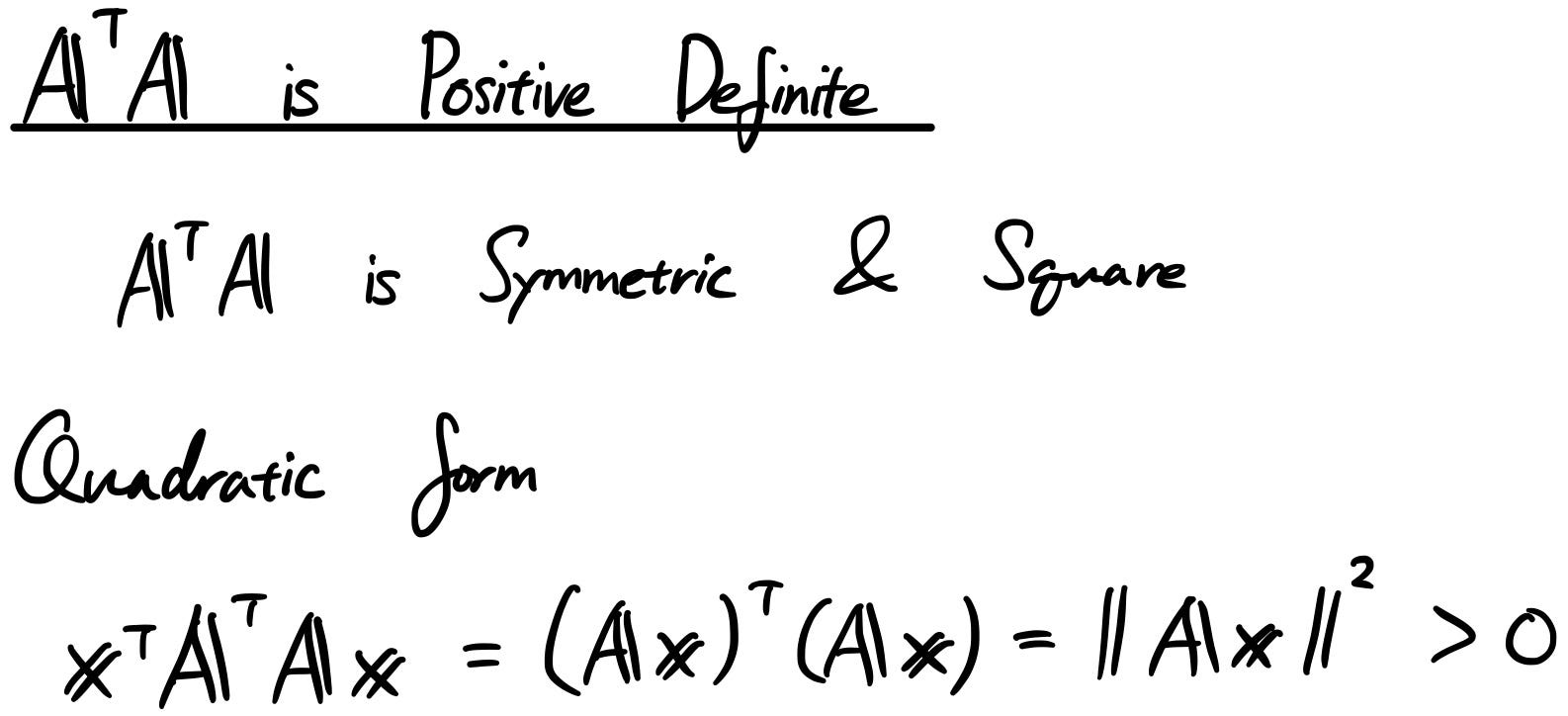
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Notation For The Set Of Symmetric Matrices And Symmetric Positive Definite Matrices Mathematics Stack Exchange

Prove That Determinant Of A 2x2 Symmetric Positive Definite Matrix Is Positive By Completing The Square Method Mathematics Stack Exchange

Test For Definiteness Of Matrix Ppt Video Online Download