Symmetric Matrix Transpose Properties
If the matrix is invertible then the inverse matrix is a symmetric matrix. For every square matrix A the sum A AT is symmetric.

Symmetric Matrix Don T Memorise Youtube
NT 2 7 3 7 9 4 3 4 7 Observe that when a matrix is symmetric as in these cases the matrix is equal to its transpose that is M MT and N NT.

Symmetric matrix transpose properties. Ie AT ij A ji ij. If the entries of A are real this becomes Ax λx. C If n -dimensional vectors v 1 v 2 v 3 are linearly dependent then the vectors v 1 v 2 v 3 v 4 is.
The eigenvalue of the symmetric matrix should be a real number. Jan 7 7 min read Matrix transposes and symmetric matrices are linked in fact the definition of a symmetric matrix is that a symmetric matrix As transpose gives back the same matrix A. Because A is symmetric we now have xTA T x λ.
Transpose of a Matrix Properties February 17 2021 by Electricalvoice A matrix obtained as a resultant by changing rows into columns and columns into rows of any matrix is known as the transpose of a matrix. A There is a 3 3 homogeneous system that has exactly three solutions. I Transpose of the Transpose Matrix.
If the entries of A are real this becomes Ax λx. The transpose of a 1 n row vector is an n 1 column vector. Suppose A is symmetric and Ax λx.
Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. For the second one be careful about the entries on the diagonal b What is the relationship between a square symmetric matrix and its transpose. Then we can conjugate to get Ax λx.
A Give a symmetric 22 matrix and an antisymmetric 22 matrix. Then start by expressing the property you want to prove in terms of a matrix transpose and use a property that you have seen in Lecture 19. A square matrix A is symmetric if and only if AT A.
Suppose A is symmetric and Ax λx. B If A and B are n n symmetric matrices then the sum A B is also symmetric. For a square matrix A the transpose AT satis es Auv uATv for any vectors uand v.
Then we can conjugate to get Ax λx. This proves that complex eigenvalues of real valued matrices come in conjugate pairs Now transpose to get xT AT xTλ. The transpose of an m 1 column vector is a 1 m row vector.
Taking the transpose of each of these produces MT 4 1 1 9. It is generally denoted by P T or P where P is any matrix. Every matrix A has a transpose AT.
Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. Why are the eigenvalues of a symmetric matrix real. Properties of Transpose of a Matrix.
Recall that a matrix A is symmetric if and only if A AT. For every matrix A we have ATT A. Determine whether each of the following sentences is true or false.
The matrix measure induced by the 2-norm ie the Euclidean norm is denoted by 2 A and 2 A 1 2 1A A0Properties of the matrix measure can be found in 11 and 12. Prove that the inverse of every invertible symmetric matrix is symmetric. A matrix is antisymmetric if each i j entry is the negative of the j i.
The matrix inverse is equal to the inverse of a transpose. If A is any symmetric matrix then A AT wwwmathcentreacuk 1 c mathcentre 2009. Some properties of transpose of a matrix are given below.
Some of the symmetric matrix properties are given below. This proves that complex eigenvalues of real valued matrices come in conjugate pairs Now transpose to get xT AT xTλ. In other words the transpose is what allows you to move the matrix from one factor in a dot product to the other factor.
Why are the eigenvalues of a symmetric matrix real. Let us now illustrate the proof that the inverse. Because A is symmetric we now have xTA T x λ.
To understand the properties of transpose matrix we will take two matrices A and B which have equal order. The j i entry. Let denote the matrix measure induced by some vector or matrix norm and defined by the formula A lim 0 jj I A jj 1.
The symmetric matrix should be a square matrix. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Symmetric Matrices Now we come to properties of symmetric matrices starting with a basic observation about trans-poses in general.
If we take transpose of transpose matrix the matrix obtained is equal to the original matrix. Winfried Just Ohio University MATH3200.
Symmetric Matrices Linear Algebra

Chapter 3 Exercise 3 3 Matrices Basics Class 12 Maths Ncert Class 12 Maths Maths Solutions Mr Math

Chapter 7 Symmetric Matrices And Quadratic Forms Flashcards Quizlet

Pdf Unitary Equivalence To A Complex Symmetric Matrix Geometric Criteria Semantic Scholar

Matrix Transposes And Symmetric Matrices By Adam Dhalla Medium

Skew Symmetric Matrices Lesson Robot Academy

Class 12 Symmetric And Skew Symmetric Matrices Youtube

1 7 Diagonal Triangular And Symmetric Matrices Diagonal

Orthogonal Matrices Symmetric Matrices Hungyi Lee Outline Orthogonal
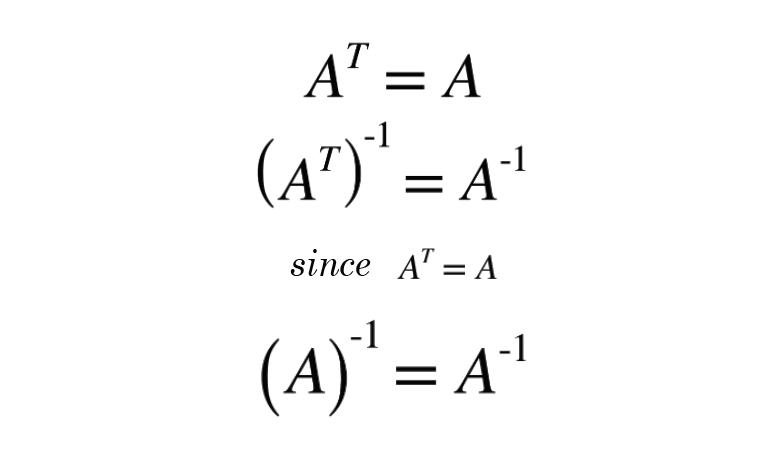
Matrix Transposes And Symmetric Matrices By Adam Dhalla Medium

Symmetric And Skew Symmetric Matrices Lecture 6 Youtube

Cbse Class 12 Maths Chap 3 Matrices Exe 3 2 Multiplication Of Matrices Cbse Class 12 Maths Class 12 Maths 12th Maths

Sec 2 3 Symmetric Matrices Youtube

Linear Algebra Symmetric Matrix Youtube

How To Prove A Matrix Is Symmetric Youtube

Symmetric And Skew Symmetric Matrices With 10 Practice Problems 6 Matrices Class 12 Youtube

1 7 Diagonal Triangular And Symmetric Matrices Diagonal

