Square Matrix Singular Value Decomposition
The Singular Value Decomposition is a highlight of linear algebraAis anymbynmatrixsquare or rectangular. Mn m n note that singular value decomposition is strictly weaker than the spectral theorem since the orthogonal matrices whose existence is ensured by singular value decomposition are not necessarily related whereas in the spectral theorem one orthogonal matrix is inverse to the other.

Understanding Singular Value Decomposition And Its Application In Data Science By Reza Bagheri Towards Data Science
Also singular value decomposition is de ned for all matrices rectangular or square unlike the more commonly used spectral decomposition in Linear Algebra.

Square matrix singular value decomposition. Singular value decomposition and inverse of square matrix. A UΣVT where U is orthogonal Σ is diagonal and V is orthogonal. They are usually not orthogonal thereare not always enough eigenvectors andAxλxrequiresAto be a square matrix.
Symmetric matrices have the nice property that their eigenvectors form an orthonormal basis. ThenAcan be factored as. The number lambda is called the eigenvalue of A corresponding to v.
We know that if A. S svd A returns the singular values of matrix A in descending order. The singular value decomposition SVD provides a matrix factorization related tothe eigenvalue decomposition that works for all matrices.
For a matrixAof rankr we can group thernon-zeroeigenvalues in anrrdiagonal matrixΛand their eigenvectors in annrmatrixE and we have. This preview shows page 130 - 132 out of 171 pages. The eigenvalue decomposition of a square matrix is of great importance and widely used.
An eigenvectoreofAis a vector that is mapped to a scaled version of itselfieAeλe whereλis the corresponding eigenvalue. Clustering The Singular Value Decomposition SVD and its Application to PCA. In contrast the columns of V in the singular value.
The reader familiar with eigenvectors and eigenvalues we do not assume familiarity here will also realize that we need conditions on the matrix to ensure orthogonality of eigenvectors. It also very helpful for analyzing properties of. Examples are presented based on over and under determined systems.
In matrixnotationAUDVT where the columns of UandVconsist of the left and right singularvectors respectively and is a diagonal matrix whose diagonal entries are the singularvalues of A. Ive implemented the SVD algorithm and began to receive wrong results so I fed my test examples to Matlab and was surprised to find that M 1 V S 1 U T. There and subsequently on other places Ive learned that if a SVD is applied to a square matrix M M U S V T then the inverse of M is relatively easy to calculate as M 1 V S 1 U T.
The singu-lar value decomposition technique is explained and related to solving linear systems of equations. However for an non-square matrix no eigenvalues and eigenvector exist. SVD of a square matrix The case where A is an n x n square matrix is of partiicular interest.
LetAbe a matrix inCmn. We will diagonalize thisA but not byX1AXThe eigenvectors inXhave three big problems. This is the final and best factorization of a matrix.
CUR decomposition wikipedia An eigenvector of a square matrix A is a non-zero vector v that when multiplied by A yields the original vector multiplied by a single number lambda. In general any matrixA2Cmncan be factored into a product of unitary matrices and a diagonal matrixas explained below. That is Av lambdav.
To get the singular value decomposition we can take advantage of the fact that for any matrix A A T A is symmetric since A T A T A T A T T A T A. 124 Jonathan Richard Shewchuk 21 The Singular Value Decomposition. Ive previously touched the subject in this question.
Square-symmetric matrices such as spectral decomposition. The eigenvalue decomposition applies to mappings fromRnto itself ie a linear operatorA. In this case we can still find its singular values and the corresponding left and right singular vectors and then carry out singular value decomposition SVD.
Rn Rndescribed by a square matrix. The singular value decomposition SVD of a matrixAis very useful in the context of least squaresproblems. 1 Introduction The Singular.
In the decomoposition A UΣVT A can be any matrix. Singular value decomposition takes a rectangular matrix of gene expression data defined as A where A is an x p matrix in which the n rows represents the genes and the p columns represents. Thesingular vectorsofAsolve all those problems in a.
This isnt terribly hard to. Singular value decomposition The singular value decomposition of a matrix is usually referred to as the SVD. Clustering The Singular Value Decomposition SVD and its Application to PCA Jonathan Richard Shewchuk 21 The Singular Value Decomposition.
In this case the Singular Value Decomposition of A is given A USVT Where V and U are orthogonal matrices.

How To Calculate The Singular Values Of A Matrix Youtube
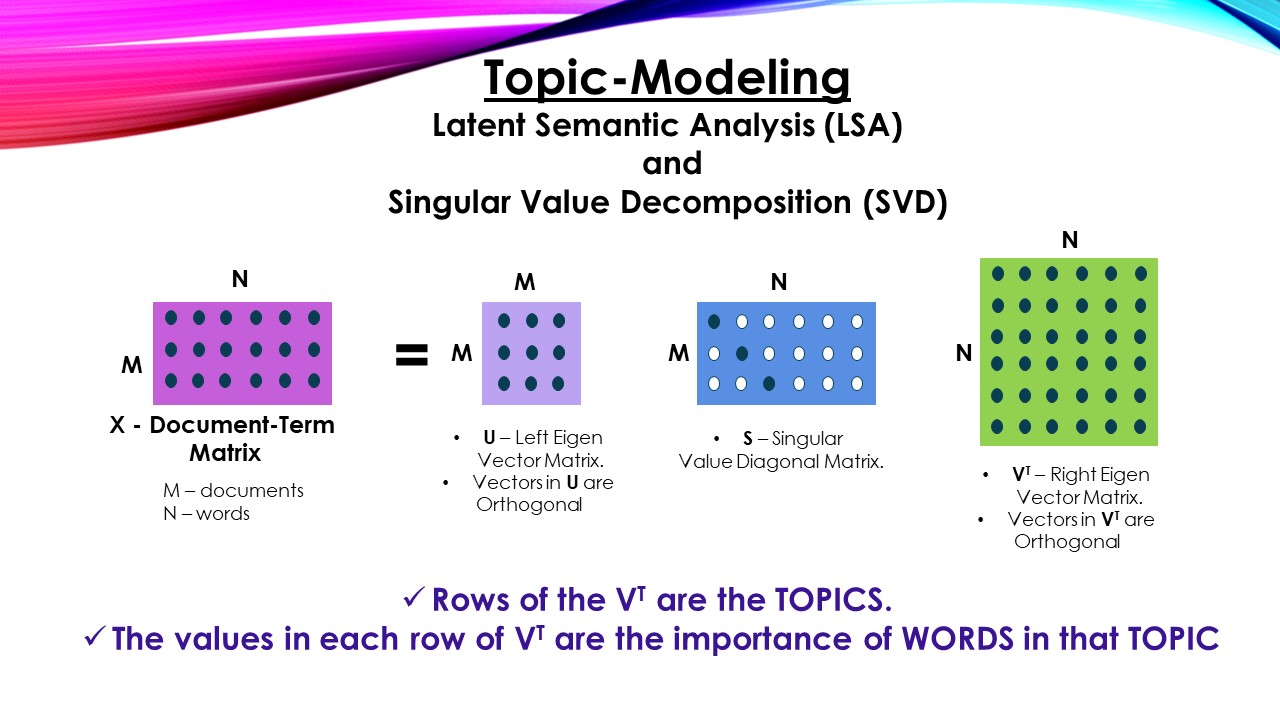
Latent Semantic Analysis Lsa And Singular Value Decomposition Svd Datajango
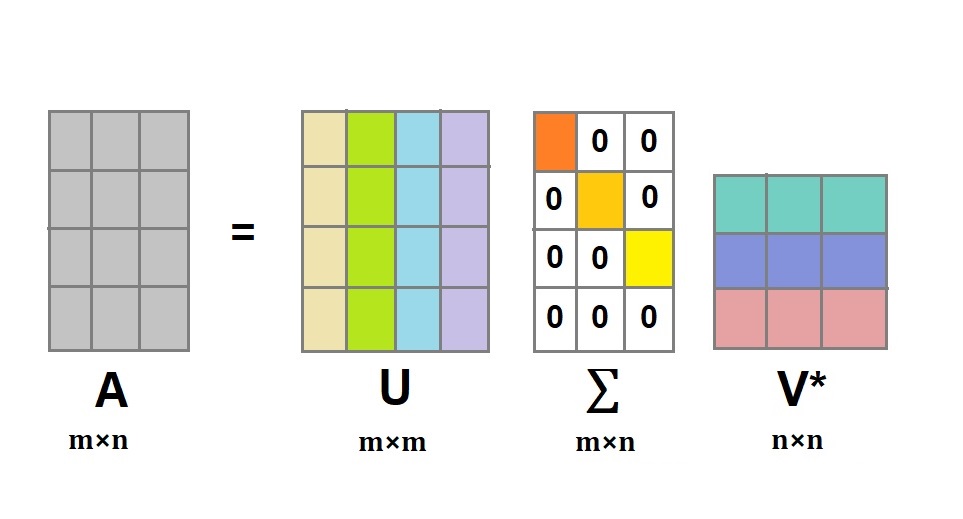
Singular Value Decomposition Svd In Python Askpython
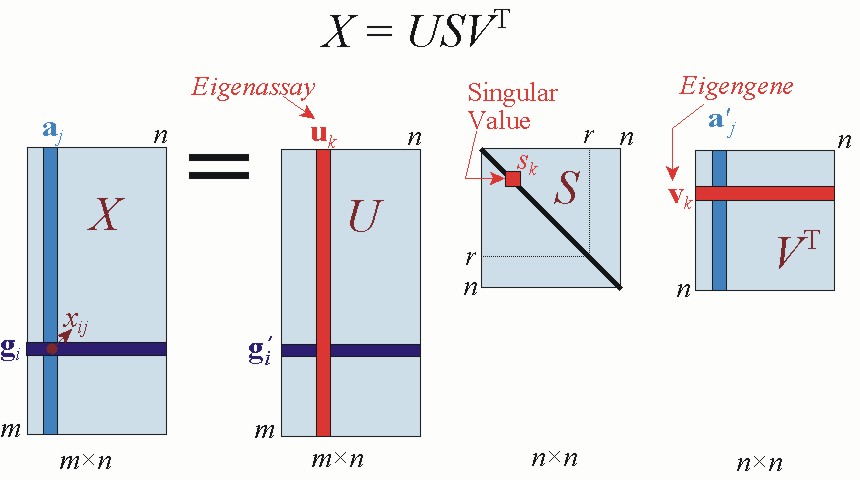
Singular Value Decomposition And Principal Component Analysis
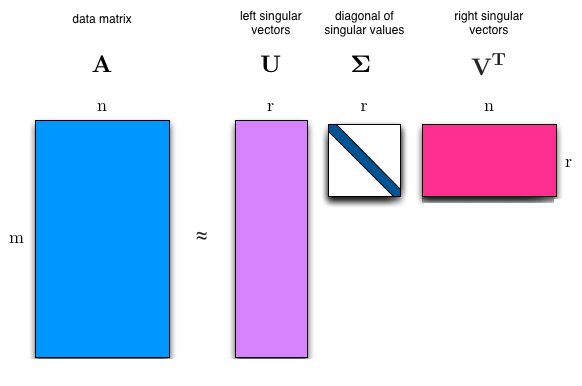
Singular Value Decomposition With Tensorflow 2 0 By Mukesh Mithrakumar Medium

Singular Value Decomposition Wikiwand

The Singular Value Decomposition Svd Of An M N Rectangular Matrix A Download Scientific Diagram
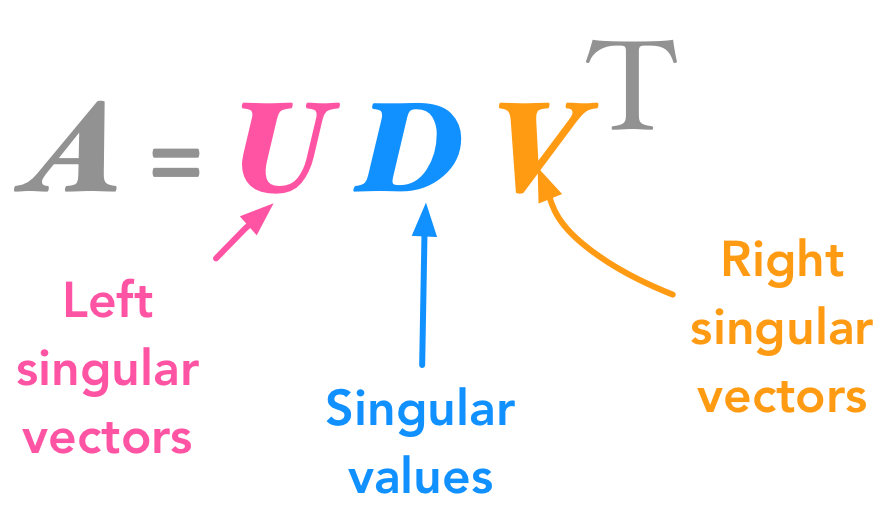
Introduction To Singular Value Decomposition Using Python Numpy Examples And Drawings

Eigen Decomposition And Singular Value Decomposition Based On

Singular Value Decomposition Ppt Video Online Download

Term Document Matrices And Singular Value Decompositions

Singular Value Decomposition Wikiwand

Eigen Decomposition And Singular Value Decomposition Based On
Everything You Need To Know About Matrix In Machine Learning Ii Eigendecomposition And Singular Value Decomposition Ju Yang
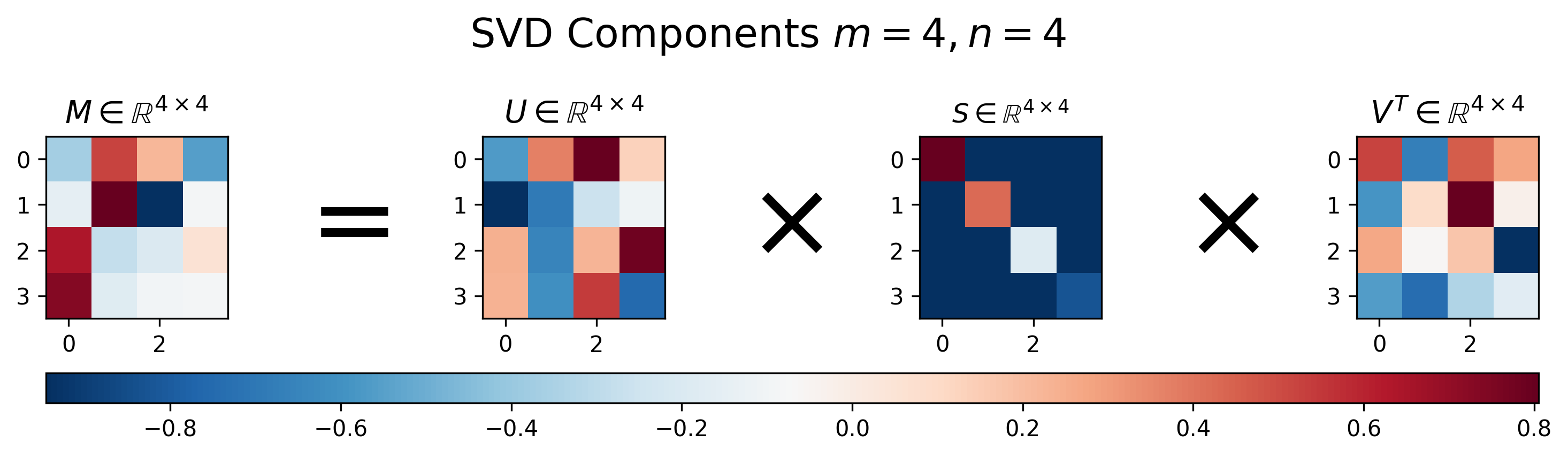
Singular Value Decomposition The Swiss Army Knife Of Linear Algebra The Clever Machine

Schematic Representation For Singular Value Decomposition Svd Download Scientific Diagram

Adel Ahmadyan Singular Value Decomposition In Computer Vision
The Singular Value Decomposition Guzinta Math

Singular Value Decomposition Wikiwand
