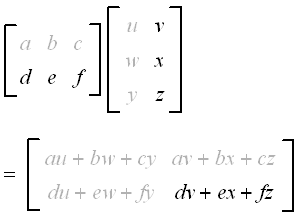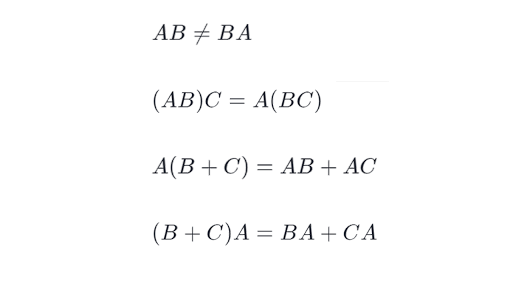Matrix Multiplication Commutative Examples
GATE 1996 Discrete and Engineering Mathematics Linear AlgebraThe matricescostheta -sinthetasintheta costhetaANDa 00 bcommute under multip. AB BA in general.
4 Multiplication Of Matrices
In this section we will show you few examples with different kinds of matrices.
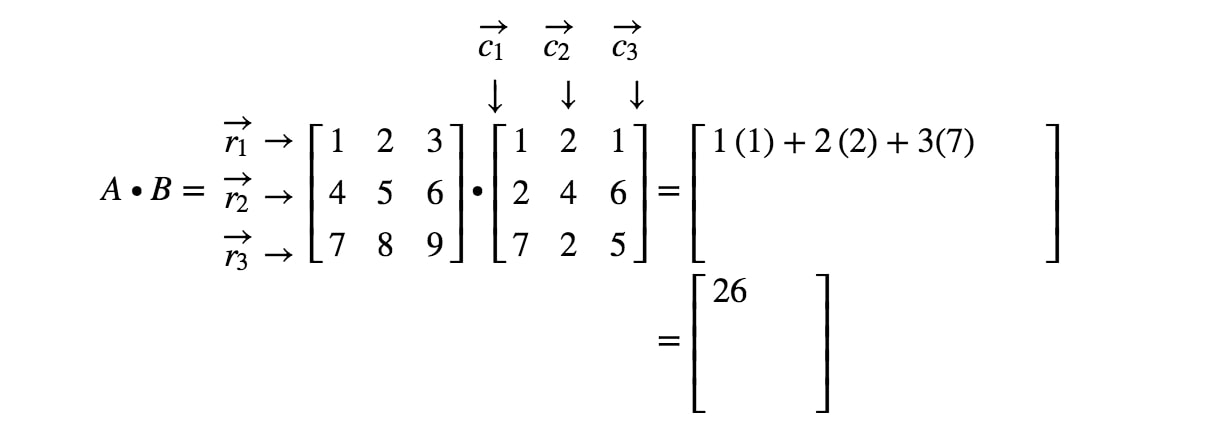
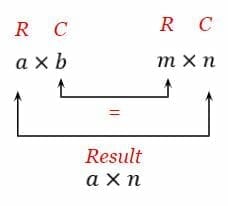
Matrix multiplication commutative examples. For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix. E latex and latexF E latexandlatexF in that order. Assuming one has to explain matrix multiplication to someone who has not seen much of linear algebra a matrix is introduced as a collection of vectors.
3 The matrices given are rotation matrices. Most familiar as the name of the property that says 3 4 4 3 or 2 5 5 2 the property can also be used in more advanced settings. Therefore resultant matrix after multiplication has a size of where.
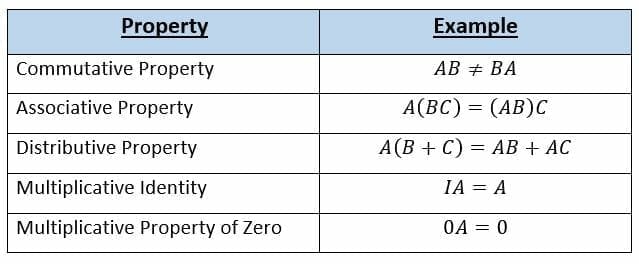
It doesnt matter which order you multiply the numbers in the result is the same. Properties of Matrix Multiplication 1. The size of matrix is where and size of matrix is also where.
In other words. Matrix multiplication can be commutative in the following cases. Link of Examples of Matrix Multiplication is given belowhttpsyoutube3ZU812qp9-ELink of Equality of matrices is given belowhttpsyoutubeGbrs1D5l9-Q.
E l a t e x a n d l a t e x F. Matrix multiplication is not in general commutative. The product of matrices A and B is denoted as AB.
Multiplying Square Matrix. To focus on square matrices and take the simple example of 2 2 ones we have. 2 One of the given matrices is a zero matrix.
Matrix multiplication is not commutative You know from grade school that the product 2 3 3 2. It is a fundamental property of many binary operations and many mathematical proofs depend on it. Just to remind you real numbers are commutative under multiplication operation which means that the order of multiplication does not affect the final product.
The resulting matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix. There are some exceptions however most notably the identity matrices that is the n by n matrices I n which consist of 1s along the main diagonal and 0 for all other entries and which act as the multiplicative identity for matrices In general when taking the product of two matrices A and B where A is a matrix with m rows and n columns and B is a matrix with n rows and p columns the resultant matrix. Multiplication of matrices generally is not commutative ie.
For example for two 3 3 matrices A and B A r A 1 r A 2 r A 3 c A 1 c A 2 c A 3 where r A i c A. In mathematics a binary operation is commutative if changing the order of the operands does not change the result. 1 One of the given matrices is an identity matrix.
In mathematics particularly in linear algebra matrix multiplication is a binary operation that produces a matrix from two matrices. Indeed as you can multiply an n m matrix by an m p one but not vice versa it may be that the multiplication A B is defined but B A is not. This does not work in general for matrices.
In general matrix multiplication is not commutative. Dec 11 2014.
Pin On Math Education
Matrix Multiplication Explanation Examples
Matrix Multiplication Explanation Examples
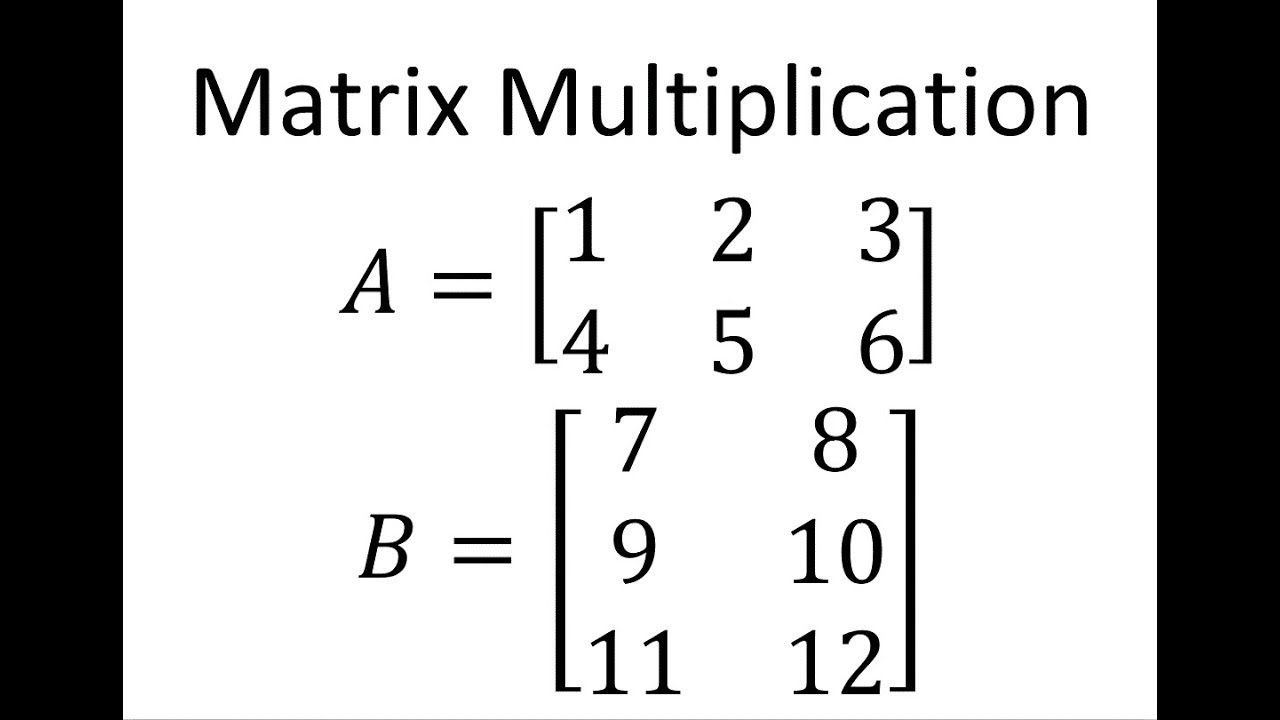
Matrix Multiplication 2x3 Times A 3x2 Youtube
3 4a Matrix Operations Finite Math
Pin On Matrices Math
Properties Of Matrix Multiplication Article Khan Academy
Pin On Algebra 2
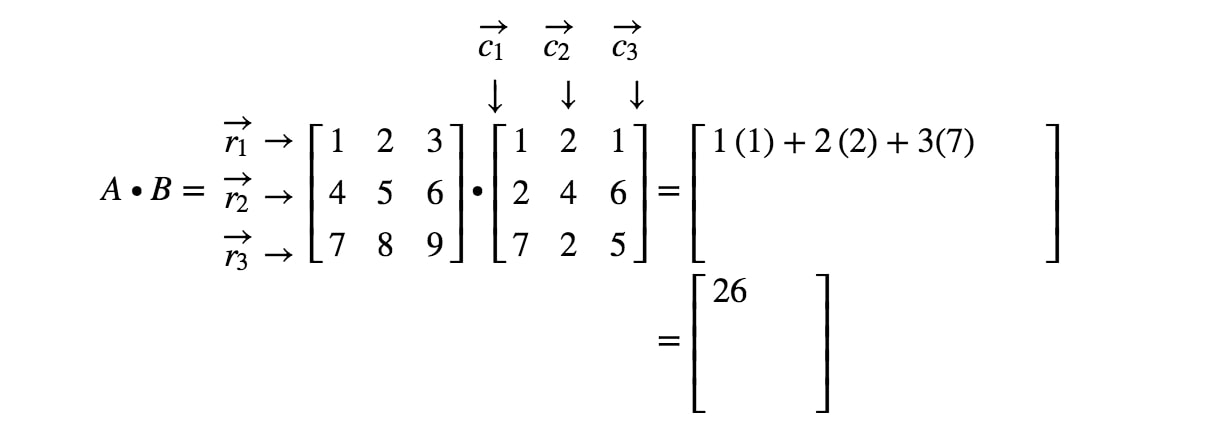
How To Multiply Two Matrices Together Studypug
Mega Matrix Multiplication
Is Matrix Multiplication Commutative Video Khan Academy
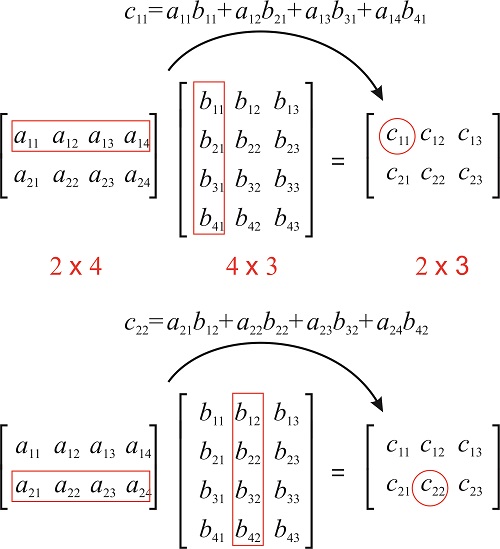
15 3 Matrix Multiplication Chemistry Libretexts
Pin On Algebra
Matrix Multiplication All Types With 10 Examples 3 Matrices Class 12 Youtube
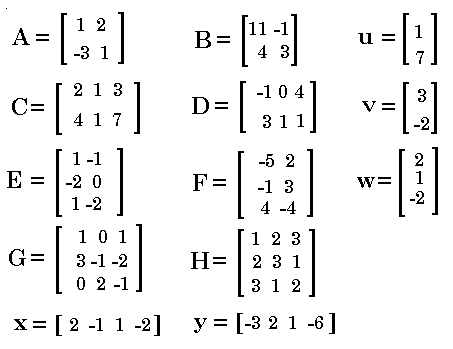
Matrix Multiplication Identity Matrices More Transpositions
Pin On Math Aids Com
An Intuitive Guide To Linear Algebra Algebra Matrix Multiplication Linear
Pin On Mathematics
Pin On Education Teaching Ideas
